Trắc nghiệm Bài 6: Trường hợp đồng dạng thứ nhất của tam giác Toán 8 Cánh diều
Đề bài
Hai tam giác vuông đồng dạng với nhau khi:
-
A.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này lần lượt tỉ lệ với hai cạnh góc vuông của tam giác kia
-
B.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này lần lượt nhỏ hơn với cạnh huyền và một cạnh góc vuông của tam giác kia
-
C.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia
-
D.
Cả A, B, C đều sai
-
A.
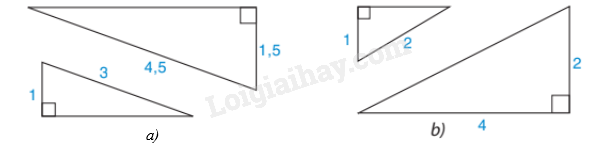
Hình a thể hiện hai tam giác đồng dạng
-
B.
Hình b thể hiện hai tam giác đồng dạng
-
C.
Cả hình a, b đều thể hiện hai tam giác đồng dạng
-
D.
Cả hình a, b đều không thể hiện hai tam giác đồng dạng
Cho tam giác ABC vuông tại A có: \(AB = 3cm,BC = 5cm\) và tam giác MNP vuông tại M có \(MN = 6cm,NP = 10cm.\) Khi đó,
-
A.
\(\Delta ABC = \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta MNP\)
-
C.
\(\Delta BAC \backsim \Delta MNP\)
-
D.
\(\Delta BCA \backsim \Delta MNP\)
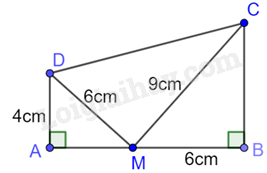
Cho hai tam giác vuông ABC và ADE có các kích thước như hình dưới. Khẳng định nào sau đây đúng?
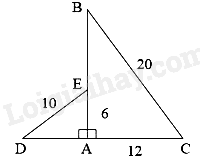
-
A.
\(\Delta ADE \backsim \Delta BAC\)
-
B.
\(\Delta ADE \backsim \Delta ABC\)
-
C.
\(\Delta ADE \backsim \Delta CBA\)
-
D.
Không có hai tam giác nào đồng dạng với nhau
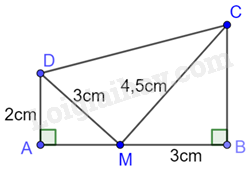
Cho tứ giác ABCD có \(AB = 9cm,\;AC = 6cm,AD = 4,\widehat {ADC} = \widehat {ACB} = {90^0}\) (như hình vẽ)
Khẳng định nào sau đây đúng?
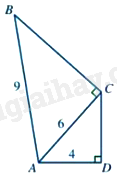
-
A.
\(\widehat {BAC} = \widehat {CAD}\)
-
B.
\(\widehat {BAC} = \frac{2}{3}\widehat {CAD}\)
-
C.
\(\frac{2}{3}\widehat {BAC} = \widehat {CAD}\)
-
D.
\(\widehat {BAC} = \frac{3}{4}\widehat {CAD}\)
-
A.
\(\widehat {DMC} = {80^0}\)
-
B.
\(\widehat {DMC} = {90^0}\)
-
C.
\(\widehat {DMC} = {100^0}\)
-
D.
\(\widehat {DMC} = {70^0}\)
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\frac{{AB}}{{DE}} = \frac{{BC}}{{FE}}\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\) Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Số đo góc ABD bằng bao nhiêu độ?
-
A.
80\(^0\).
-
B.
90\(^0\).
-
C.
95\(^0\).
-
D.
85\(^0\).
Tam giác ABH vuông tại H có \(AB = 20cm,BH = 12cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(AC = \frac{5}{3}AH.\) Khi đó, số đo góc BAC bằng:
-
A.
80\(^0\)
-
B.
90\(^0\)
-
C.
95\(^0\)
-
D.
85\(^0\)
Cho tam giác ABC cân tại A, đường cao AH và M là trọng tâm của tam giác ABC; tam giác A’B’C’ cân tại A’, đường cao A’H và M’ là trọng tâm tâm của tam giác A’B’C’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{AB}}{{A'B'}} = 3.\) Chọn đáp án đúng.
-
A.
\(\frac{{BM}}{{B'M'}} = \frac{7}{4}\)
-
B.
\(\frac{{BM}}{{B'M'}} = \frac{5}{2}\)
-
C.
\(\frac{{BM}}{{B'M'}} = \frac{3}{2}\)
-
D.
\(\frac{{BM}}{{B'M'}} = 3\)
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\)Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Diện tích tam giác ABD bằng:
-
A.
\(9\sqrt {20} c{m^2}\)
-
B.
\(\frac{9}{2}\sqrt {20} c{m^2}\)
-
C.
\(\sqrt {20} c{m^2}\)
-
D.
\(\frac{9}{4}\sqrt {20} c{m^2}\)
Tam giác ABH vuông tại H có \(AB = 25cm,BH = 15cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(AC = \frac{5}{3}AH.\) Chu vi tam giác AHC là:
-
A.
80cm
-
B.
90cm
-
C.
70cm
-
D.
100cm
-
A.
\(15 - \sqrt {117} cm\)
-
B.
\(15 + \sqrt {117} cm\)
-
C.
\(15 + \sqrt {118} cm\)
-
D.
\(15 - \sqrt {118} cm\)
Cho tam giác ABC cân tại A có chu vi bằng 60cm và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{BC}}{{B'C'}} = \frac{3}{2}\). Chu vi tam giác A’B’C’ là:
-
A.
15cm
-
B.
20cm
-
C.
30cm
-
D.
40cm
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{CH}}{{C'H'}} = \frac{{BC}}{{B'C'}}\). Biết rằng \(\widehat {BAC} = 4\widehat {A'C'B'}.\) Chọn đáp án đúng.
-
A.
\(\widehat {BAC} = {90^0}\)
-
B.
\(\widehat {BAC} = {100^0}\)
-
C.
\(\widehat {BAC} = {120^0}\)
-
D.
\(\widehat {BAC} = {110^0}\)
Cho điểm B nằm trên đoạn thẳng AC sao cho \(AB = 6cm,BC = 24cm.\) Vẽ về một phía của AC tia Ax và Cy vuông góc với AC. Trên tia Ax lấy điểm E sao cho \(EB = 10cm,\) trên tia Cy lấy điểm D sao cho \(BD = 30cm.\)
Cho các khẳng định sau:
1. Tam giác EBD là tam giác nhọn.
2. Diện tích tam giác EBD bằng \(150c{m^2}\).
3. Chu vi tam giác EBD bằng 60cm.
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Cho hai hình chữ nhật ABCD và A’B’C’D’ thỏa mãn \(AC = 3AB,B'D' = 3A'B'\)
Nếu \(AB = 2A'B'\) và diện tích hình chữ nhật ABCD là \(12{m^2}\) thì diện tích hình chữ nhật A’B’C’D’ là bao nhiêu?
-
A.
\(6{m^2}\)
-
B.
\(8{m^2}\)
-
C.
\(10{m^2}\)
-
D.
\(3{m^2}\)
Trong các cặp tam giác sau cặp tam giác nào đồng dạng nếu các cạnh của hai tam giác có độ dài là :
-
A.
\(3cm;4cm;6cm\) và \(9cm;15cm;18cm\) .
-
B.
\(4cm;5cm;6cm\) và \(8cm;10cm;12cm\) .
-
C.
\(6cm;5cm;6cm\) và \(3cm;5cm;3cm\) .
-
D.
\(5cm;7cm;1dm\) và \(10cm;14cm;18cm\) .
Cho tam giác ABC có AB = 6cm; AC = 9cm; BC = 12cm và tam giác MNP có NP = 8cm; MN= 12cm; PM = 16cm. khẳng định nào sau đây là đúng?
-
A.
\(\Delta ABC \backsim \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta NMP\)
-
C.
\(\Delta ABC \backsim \Delta NPM\)
-
D.
\(\Delta BAC \backsim \Delta MNP\)
Với điều kiện nào sau đây thì \(\Delta ABC \backsim \Delta MNP\)
-
A.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) .
-
B.
\(\frac{{AB}}{{MP}} = \frac{{AC}}{{MN}} = \frac{{BC}}{{NP}}\) .
-
C.
\(\frac{{AB}}{{NP}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{MN}}\) .
-
D.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MP}}\) .
Cho \(\Delta ABC \backsim \Delta MNP\) biết \(AB = 3cm;BC = 4cm;MN = 6cm;MP = 5cm\) . Khi đó:
-
A.
AC = 8cm; NP = 2,5cm
-
B.
AC = 2,5cm; NP = 8cm
-
C.
AC = 2,5cm; NP = 10cm
-
D.
AC = 10cm; NP = 2cm
Cho tam giác ABC có AB = 3cm, AC = 5cm; BC = 7cm và MNP có MN = 6cm;
MP = 10cm; NP = 14cm. Tỉ số chu vi của hai tam giác ABC và MNP là
-
A.
\(\frac{3}{5}\) .
-
B.
2.
-
C.
\(\frac{5}{6}\) .
-
D.
\(\frac{1}{2}\) .
Cho hai tam giác ABC và DEF có kích thước như trong hình, hai tam giác có đồng dạng với nhau không, nếu có thì tỉ số đồng dạng là bao nhiêu?
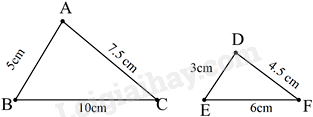
-
A.
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) tỉ số đồng dạng là 2.
-
B.
Hai tam giác không đồng dạng.
-
C.
\(\Delta ABC \backsim \Delta {\rm{FED}}\) tỉ số đồng dạng là \(\frac{5}{3}\) .
-
D.
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) tỉ số đồng dạng là \(\frac{5}{3}\) .
-
A.
\(\Delta ABC \backsim \Delta DBC\)
-
B.
\(\Delta A{\rm{D}}B \backsim \Delta DBC\)
-
C.
\(\Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C\)
-
D.
\(\Delta A{\rm{D}}C \backsim \Delta ABC\)
Cho tam giác ABC có AB = 3cm; AC = 6cm; BC = 9cm và MNP có MN = 1cm; MP = 2cm; NP = 3cm. Tỉ số chu vi của hai tam giác MNP và ABC là
-
A.
\(\frac{1}{2}\) .
-
B.
3.
-
C.
\(\frac{1}{3}\) .
-
D.
2.
Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) khẳng định nào sau đây là sai
-
A.
\(\frac{{AB}}{{{A_1}{B_1}}} = \frac{{AC}}{{{A_1}{C_1}}} = \frac{{BC}}{{{B_1}{C_1}}}\) .
-
B.
\(\frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}}\) .
-
C.
\(\frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{A_1}{B_1}}}{{AB}}\) .
-
D.
\(\frac{{AB}}{{{A_1}{B_1}}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{BC}}{{{B_1}{C_1}}}\) .
Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với \(4:5:6\) . Cho biết \(\Delta ABC \backsim \Delta A'B'C'\) và cạnh nhỏ nhất của \(\Delta A'B'C'\) bằng 2cm. Độ dài các cạnh còn lại của tam giác \(A'B'C'\) lần lượt là
-
A.
3cm; 4cm
-
B.
2,5cm; 4cm.
-
C.
3cm; 2cm
-
D.
2,5cm; 3cm.
Tam giác thứ nhất có cạnh nhỏ nhất bằng 8cm, hai cạnh còn lại bằng x và y (x < y). Tam giác thứ hai có cạnh lớn nhất bằng 27cm hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đồng dạng:
-
A.
x = 12cm; y = 18cm
-
B.
x = 9cm; y = 24cm
-
C.
x = 18cm; y = 12cm
-
D.
x = 8cm; y = 27cm
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Cho biết tam giác ABC có chu vi bằng 450cm, chu vi tam giác PQR có độ dài là
-
A.
220cm
-
B.
900cm
-
C.
225cm
-
D.
150cm
Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm và tam giác A’B’C’ vuông tại A’ có A’B’= 3cm; A’C’ = 4cm. Tam giác ABC đồng dạng với tam giác A’B’C’ không và nếu có thì tỉ số chu vi của hai tam giác là bao nhiêu?
-
A.
\(\Delta ABC \backsim \Delta A'B'C'\) tỉ số chu vi của hai tam giác là 2.
-
B.
Hai tam giác không đồng dạng.
-
C.
\(\Delta ABC \backsim \Delta A'B'C'\) tỉ số chu vi của hai tam giác là 3.
-
D.
\(\Delta ABC \backsim \Delta A'B'C'\) tỉ số chu vi của hai tam giác là \(\frac{3}{2}\) .
Lời giải và đáp án
Hai tam giác vuông đồng dạng với nhau khi:
-
A.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này lần lượt tỉ lệ với hai cạnh góc vuông của tam giác kia
-
B.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này lần lượt nhỏ hơn với cạnh huyền và một cạnh góc vuông của tam giác kia
-
C.
Cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác kia
-
D.
Cả A, B, C đều sai
Đáp án : C
-
A.
Hình a thể hiện hai tam giác đồng dạng
-
B.
Hình b thể hiện hai tam giác đồng dạng
-
C.
Cả hình a, b đều thể hiện hai tam giác đồng dạng
-
D.
Cả hình a, b đều không thể hiện hai tam giác đồng dạng
Đáp án : A
Hình b không thể hiện hai tam giác đồng dạng
Cho tam giác ABC vuông tại A có: \(AB = 3cm,BC = 5cm\) và tam giác MNP vuông tại M có \(MN = 6cm,NP = 10cm.\) Khi đó,
-
A.
\(\Delta ABC = \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta MNP\)
-
C.
\(\Delta BAC \backsim \Delta MNP\)
-
D.
\(\Delta BCA \backsim \Delta MNP\)
Đáp án : B
Do đó, \(\Delta ABC \backsim \Delta MNP\)
Cho hai tam giác vuông ABC và ADE có các kích thước như hình dưới. Khẳng định nào sau đây đúng?

-
A.
\(\Delta ADE \backsim \Delta BAC\)
-
B.
\(\Delta ADE \backsim \Delta ABC\)
-
C.
\(\Delta ADE \backsim \Delta CBA\)
-
D.
Không có hai tam giác nào đồng dạng với nhau
Đáp án : B
Ta có: \(\frac{{AE}}{{AC}} = \frac{6}{{12}} = \frac{1}{2};\frac{{DE}}{{BC}} = \frac{{10}}{{20}} = \frac{1}{2}\) nên \(\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\)
Tam giác ADE và tam giác ABC có: \(\widehat {DAE} = \widehat {BAC} = {90^0},\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\) nên \(\Delta ADE \backsim \Delta ABC\)
Cho tứ giác ABCD có \(AB = 9cm,\;AC = 6cm,AD = 4,\widehat {ADC} = \widehat {ACB} = {90^0}\) (như hình vẽ)
Khẳng định nào sau đây đúng?

-
A.
\(\widehat {BAC} = \widehat {CAD}\)
-
B.
\(\widehat {BAC} = \frac{2}{3}\widehat {CAD}\)
-
C.
\(\frac{2}{3}\widehat {BAC} = \widehat {CAD}\)
-
D.
\(\widehat {BAC} = \frac{3}{4}\widehat {CAD}\)
Đáp án : A
Xét tam giác ADC và tam giác ACB có: \(\widehat {ADC} = \widehat {ACB} = {90^0}\), \(\frac{{AC}}{{AB}} = \frac{{AD}}{{AC}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta ADC \backsim \Delta ACB.\)
Do đó, \(\widehat {BAC} = \widehat {CAD}\)
-
A.
\(\widehat {DMC} = {80^0}\)
-
B.
\(\widehat {DMC} = {90^0}\)
-
C.
\(\widehat {DMC} = {100^0}\)
-
D.
\(\widehat {DMC} = {70^0}\)
Đáp án : B
Tam giác ADM và tam giác BMC có:
\(\widehat A = \widehat B = {90^0},\frac{{AD}}{{MB}} = \frac{{DM}}{{MC}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta AMD \backsim \Delta BCM\) nên \(\widehat {ADM} = \widehat {BMC}\)
Mà: \(\widehat {AMD} + \widehat {ADM} = {90^0},\) do đó, \(\widehat {AMD} + \widehat {BMC} = {90^0}\)
Lại có: \(\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = {180^0}\)
Suy ra: \(\widehat {DMC} = {180^0} - \left( {\widehat {AMD} + \widehat {BMC}} \right) = {90^0}\)
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D có: \(\frac{{AB}}{{DE}} = \frac{{BC}}{{FE}}\)
Chọn đáp án đúng
-
A.
\(\Delta ABC = \Delta DEF\)
-
B.
\(\Delta ABC \backsim \Delta DFE\)
-
C.
\(\Delta ABC \backsim \Delta EDF\)
-
D.
\(\Delta ABC \backsim \Delta DEF\)
Đáp án : D
Tam giác ABC và tam giác DEF có: \(\widehat {BAC} = \widehat {EDF} = {90^0}, \frac{{AB}}{{DE}} = \frac{{BC}}{{FE}}\) nên \(\Delta ABC \backsim \Delta DEF\).
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\) Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Số đo góc ABD bằng bao nhiêu độ?
-
A.
80\(^0\).
-
B.
90\(^0\).
-
C.
95\(^0\).
-
D.
85\(^0\).
Đáp án : B
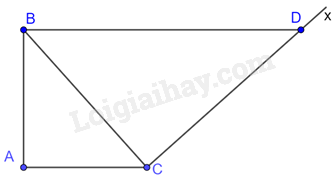
Tam giác ABC và tam giác CDB có:
\(\widehat A = \widehat {BCD} = {90^0},\frac{{AC}}{{BC}} = \frac{{BC}}{{BD}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta ABC \backsim \Delta CDB\) nên \(\widehat {ABC} = \widehat {BDC}\)
Mà \(\widehat {BDC} + \widehat {CBD} = {90^0}\) nên \(\widehat {ABC} + \widehat {CBD} = {90^0}\) hay \(\widehat {ABD} = {90^0}\)
Tam giác ABH vuông tại H có \(AB = 20cm,BH = 12cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(AC = \frac{5}{3}AH.\) Khi đó, số đo góc BAC bằng:
-
A.
80\(^0\)
-
B.
90\(^0\)
-
C.
95\(^0\)
-
D.
85\(^0\)
Đáp án : B

Ta có: \(\frac{{AB}}{{BH}} = \frac{{20}}{{12}} = \frac{5}{3};AC = \frac{5}{3}AH \Rightarrow \frac{{AC}}{{AH}} = \frac{5}{3} \Rightarrow \frac{{AB}}{{BH}} = \frac{{AC}}{{AH}} \Rightarrow \frac{{AB}}{{AC}} = \frac{{BH}}{{AH}}\)
Tam giác ABH và tam giác CAH có: \(\widehat {AHB} = \widehat {AHC} = {90^0},\frac{{AB}}{{AC}} = \frac{{BH}}{{AH}}\)
Do đó, \(\Delta ABH \backsim \Delta CAH\)
Suy ra: \(\widehat {CAH} = \widehat {ABH}\)
Mà \(\widehat {BAH} + \widehat {ABH} = {90^0}\) nên \(\widehat {BAH} + \widehat {CAH} = {90^0}\) hay \(\widehat {BAC} = {90^0}\)
Cho tam giác ABC cân tại A, đường cao AH và M là trọng tâm của tam giác ABC; tam giác A’B’C’ cân tại A’, đường cao A’H và M’ là trọng tâm tâm của tam giác A’B’C’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{AB}}{{A'B'}} = 3.\) Chọn đáp án đúng.
-
A.
\(\frac{{BM}}{{B'M'}} = \frac{7}{4}\)
-
B.
\(\frac{{BM}}{{B'M'}} = \frac{5}{2}\)
-
C.
\(\frac{{BM}}{{B'M'}} = \frac{3}{2}\)
-
D.
\(\frac{{BM}}{{B'M'}} = 3\)
Đáp án : D

Tam giác ABC cân tại A, AH là đường cao đồng thời là đường trung tuyến của tam giác. Do đó, M thuộc AH. Do đó, \(3MH = AH\)
Tam giác A’B’C’ cân tại A’, A’H’ là đường cao đồng thời là đường trung tuyến của tam giác. Do đó, M’ thuộc A’H’. Do đó, \(3M'H' = A'H'\)
Xét tam giác ABH và tam giác A’B’H’ có: \(\widehat {AHB} = \widehat {A'H'B'} = {90^0},\frac{{BH}}{{B'H'}} = \frac{{AB}}{{A'B'}} = 3\)
Suy ra: \(\Delta AHB \backsim \Delta A'H'B'\), do đó, \(\frac{{AH}}{{A'H'}} = 3 \Rightarrow \frac{{3HM}}{{3H'M'}} = 3 \Rightarrow \frac{{HM}}{{H'M'}} = 3\)
Tam giác BHM và tam giác B’H’M’ có:
\(\widehat {MHB} = \widehat {M'H'B'} = {90^0},\frac{{HM}}{{HM'}} = \frac{{BH}}{{B'H'}} = 3\)
Do đó, \(\Delta BMH \backsim \Delta B'M'H'\) nên \(\frac{{BM}}{{B'M'}} = \frac{{BH}}{{B'H'}} = 3\)
Cho tam giác ABC vuông tại A, \(AC = 4cm,BC = 6cm.\)Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy trên tia Cx điểm D sao cho \(BD = 9cm.\) Diện tích tam giác ABD bằng:
-
A.
\(9\sqrt {20} c{m^2}\)
-
B.
\(\frac{9}{2}\sqrt {20} c{m^2}\)
-
C.
\(\sqrt {20} c{m^2}\)
-
D.
\(\frac{9}{4}\sqrt {20} c{m^2}\)
Đáp án : B

Tam giác ABC và tam giác CDB có:
\(\widehat A = \widehat {BCD} = {90^0},\frac{{AC}}{{BC}} = \frac{{BC}}{{BD}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta ABC \backsim \Delta CDB\) nên \(\widehat {ABC} = \widehat {BDC}\)
Mà \(\widehat {BDC} + \widehat {CBD} = {90^0}\) nên \(\widehat {ABC} + \widehat {CBD} = {90^0}\) hay \(\widehat {ABD} = {90^0}\)
Do đó, tam giác ABD vuông tại B
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có:
\(A{B^2} + A{C^2} = B{C^2}\)
\(A{B^2} = B{C^2} - A{C^2} = 20\)
\(AB = \sqrt {20} cm\)
Do tam giác ABD vuông tại B nên diện tích tam giác ABD là:
\(\frac{1}{2}AB.BD = \frac{1}{2}.\sqrt {20} .9 = \frac{9}{2}\sqrt {20} \left( {c{m^2}} \right)\)
Tam giác ABH vuông tại H có \(AB = 25cm,BH = 15cm.\) Trên tia đối của tia HB lấy điểm C sao cho \(AC = \frac{5}{3}AH.\) Chu vi tam giác AHC là:
-
A.
80cm
-
B.
90cm
-
C.
70cm
-
D.
100cm
Đáp án : A
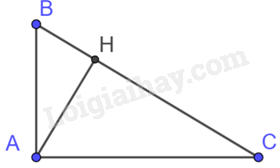
Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có: \(A{B^2} = B{H^2} + A{H^2}\)
\(A{H^2} = A{B^2} - B{H^2} = 400\) nên \(AH = 20cm \Rightarrow AC = \frac{5}{3}.20 = \frac{{100}}{3}\left( {cm} \right)\)
Ta có: \(\frac{{AB}}{{BH}} = \frac{{25}}{{15}} = \frac{5}{3};AC = \frac{5}{3}AH \Rightarrow \frac{{AC}}{{AH}} = \frac{5}{3} \Rightarrow \frac{{AB}}{{BH}} = \frac{{AC}}{{AH}} \Rightarrow \frac{{AB}}{{AC}} = \frac{{BH}}{{AH}}\)
Tam giác ABH và tam giác CAH có: \(\widehat {AHB} = \widehat {AHC} = {90^0},\frac{{AB}}{{AC}} = \frac{{BH}}{{AH}}\)
Do đó, \(\Delta ABH \backsim \Delta CAH \Rightarrow \frac{{AB}}{{AC}} = \frac{{AH}}{{CH}} \Rightarrow CH = \frac{{AH.AC}}{{AB}} = \frac{{80}}{3}cm\)
Vậy chu vi tam giác AHC là: \(AH + HC + AC = 20 + \frac{{80}}{3} + \frac{{100}}{3} = 80\left( {cm} \right)\)
-
A.
\(15 - \sqrt {117} cm\)
-
B.
\(15 + \sqrt {117} cm\)
-
C.
\(15 + \sqrt {118} cm\)
-
D.
\(15 - \sqrt {118} cm\)
Đáp án : B
Tam giác ADM và tam giác BMC có:
\(\widehat A = \widehat B = {90^0},\frac{{AD}}{{MB}} = \frac{{DM}}{{MC}}\left( { = \frac{2}{3}} \right)\)
Do đó, \(\Delta AMD \backsim \Delta BCM\) nên \(\widehat {ADM} = \widehat {BMC}\)
Mà: \(\widehat {AMD} + \widehat {ADM} = {90^0},\) do đó, \(\widehat {AMD} + \widehat {BMC} = {90^0}\)
Lại có: \(\widehat {AMD} + \widehat {DMC} + \widehat {CMB} = {180^0}\)
Suy ra: \(\widehat {DMC} = {180^0} - \left( {\widehat {AMD} + \widehat {BMC}} \right) = {90^0}\)
Do đó, tam giác DMC vuông tại M
Áp dụng định lý Pythagore vào tam giác DMC vuông tại M có:
\(D{C^2} = D{M^2} + M{C^2} = 117\) nên \(DC = \sqrt {117} cm\)
Vậy chu vi tam giác DMC là: \(DM + MC + DC = 6 + 9 + \sqrt {117} = 15 + \sqrt {117} \left( {cm} \right)\)
Cho tam giác ABC cân tại A có chu vi bằng 60cm và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{BH}}{{B'H'}} = \frac{{BC}}{{B'C'}} = \frac{3}{2}\). Chu vi tam giác A’B’C’ là:
-
A.
15cm
-
B.
20cm
-
C.
30cm
-
D.
40cm
Đáp án : D
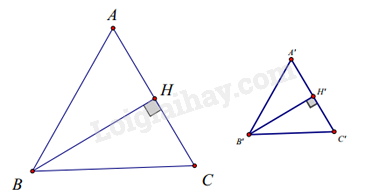
Tam giác BHC và tam giác B’H’C’ có: \(\widehat {BHC} = \widehat {B'H'C'} = {90^0},\frac{{BH}}{{B'H'}} = \frac{{BC}}{{B'C'}} = \frac{3}{2}\)
Do đó, \(\Delta BHC \backsim \Delta B'H'C'\)
Suy ra: \(\widehat C = \widehat {C'}\), mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên \(\widehat B = \widehat {B'} = \widehat C = \widehat {C'}\)
Do đó, \(\Delta ABC \backsim \Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{2}{3}\)
Theo tính chất dãy tỉ số bằng nhau ta có: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{{AB + BC + AC}}{{A'B' + B'C' + A'C'}} = \frac{2}{3}\)
Mà chu vi tam giác ABC bằng 60cm nên chu vi tam giác A’B’C’ là: \(60:\frac{3}{2} = 40\left( {cm} \right)\)
Cho tam giác ABC cân tại A và tam giác A’B’C’ cân tại A’, các đường cao BH và B’H’. Biết rằng \(\frac{{CH}}{{C'H'}} = \frac{{BC}}{{B'C'}}\). Biết rằng \(\widehat {BAC} = 4\widehat {A'C'B'}.\) Chọn đáp án đúng.
-
A.
\(\widehat {BAC} = {90^0}\)
-
B.
\(\widehat {BAC} = {100^0}\)
-
C.
\(\widehat {BAC} = {120^0}\)
-
D.
\(\widehat {BAC} = {110^0}\)
Đáp án : C
Tam giác BHC và tam giác B’H’C’ có: \(\widehat {BHC} = \widehat {B'H'C'} = {90^0},\frac{{CH}}{{C'H'}} = \frac{{BC}}{{B'C'}}\)
Do đó, \(\Delta BHC \backsim \Delta B'H'C'\)
Suy ra: \(\widehat C = \widehat {C'}\), mà tam giác ABC cân tại A, tam giác A’B’C’ cân tại A’ nên \(\widehat B = \widehat {B'} = \widehat C = \widehat {C'}\)
Do đó, \(\widehat {BAC} = 4\widehat {ACB} = 4\widehat {ABC}\)
Lại có: \(\widehat {BAC} + \widehat {ACB} + \widehat {ABC} = {180^0} \Rightarrow 6\widehat {ACB} = {180^0} \Rightarrow \widehat {ACB} = {30^0} \Rightarrow \widehat {BAC} = {120^0}\)
Cho điểm B nằm trên đoạn thẳng AC sao cho \(AB = 6cm,BC = 24cm.\) Vẽ về một phía của AC tia Ax và Cy vuông góc với AC. Trên tia Ax lấy điểm E sao cho \(EB = 10cm,\) trên tia Cy lấy điểm D sao cho \(BD = 30cm.\)
Cho các khẳng định sau:
1. Tam giác EBD là tam giác nhọn.
2. Diện tích tam giác EBD bằng \(150c{m^2}\).
3. Chu vi tam giác EBD bằng 60cm.
Trong các khẳng định trên, có bao nhiêu khẳng định đúng?
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Đáp án : B
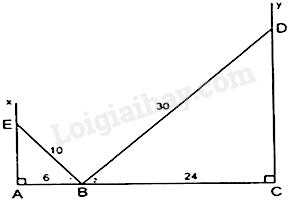
Áp dụng định lý Pythagore vào tam giác CDB vuông ở C ta có:
\(B{D^2} = D{C^2} + C{B^2}\)
\(D{C^2} = {30^2} - {24^2} = 324 \Rightarrow DC = 18cm\)
Xét tam giác BEA và tam giác DBC có:
\(\widehat A = \widehat C = {90^0},\frac{{BE}}{{BD}} = \frac{{BA}}{{DC}}\left( { = \frac{1}{3}} \right)\)
Do đó, \(\Delta BEA \backsim \Delta DBC\), suy ra \(\widehat {EBA} = \widehat {BDC}\)
Mà \(\widehat {DBC} + \widehat {BDC} = {90^0} \Rightarrow \widehat {DBC} + \widehat {EBA} = {90^0}\)
Lại có: \(\widehat {DBC} + \widehat {EBD} + \widehat {EBA} = {180^0}\) nên \(\widehat {EBD} = {90^0}\)
Do đó, tam giác BDE vuông tại B.
Diện tích tam giác EBD là: \(\frac{1}{2}BE.BD = \frac{1}{2}.10.30 = 150\left( {c{m^2}} \right)\)
Áp dụng định lý Pythagore vào tam giác EBD vuông tại B có:
\(E{D^2} = E{B^2} + B{D^2} = {10^2} + {30^2} = 1000 \Rightarrow ED = \sqrt {1000} cm\)
Chu vi tam giác EBD là: \(EB + BD + ED = 10 + 30 + \sqrt {1000} = 40 + \sqrt {1000} \left( {cm} \right)\)
Vậy có 1 khẳng định đúng.
Cho hai hình chữ nhật ABCD và A’B’C’D’ thỏa mãn \(AC = 3AB,B'D' = 3A'B'\)
Nếu \(AB = 2A'B'\) và diện tích hình chữ nhật ABCD là \(12{m^2}\) thì diện tích hình chữ nhật A’B’C’D’ là bao nhiêu?
-
A.
\(6{m^2}\)
-
B.
\(8{m^2}\)
-
C.
\(10{m^2}\)
-
D.
\(3{m^2}\)
Đáp án : D

Vì \(AC = 3AB \Rightarrow \frac{{AB}}{{AC}} = \frac{1}{3},B'D' = 3A'B' \Rightarrow \frac{{A'B'}}{{B'D'}} = \frac{1}{3}\)
Do đó, \(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{B'D'}} \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{B'D'}}\)
Tam giác ABC và tam giác A’B’D’ có:
\(\widehat {ABC} = \widehat {B'A'D'} = {90^0};\frac{{AB}}{{A'B'}} = \frac{{AC}}{{B'D'}}\) nên \(\Delta ABC \backsim B'A'D'\left( 1 \right)\)
Chứng minh được \(\Delta B'A'D' = \Delta A'B'C'\left( 2 \right)\)
Từ (1) và (2) ta có: \(\Delta ABC \backsim \Delta A'B'C'\)
Do đó, \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{2}\)
Diện tích hình chữ nhật ABCD là: \({S_{ABCD}} = AB.BC\)
Diện tích hình chữ nhật A’B’C’D’ là: \({S _{A'B'C'D'}} = A'B'.B'C'\)
Do đó: \(\frac{{{S_{ABCD}}}}{{{S_{A'B'C'D'}}}} = \frac{{AB.BC}}{{A'B'.B'C'}} = \frac{{AB}}{{A'B'}}.\frac{{BC}}{{B'C'}} = 2.2 = 4\)
\( \Rightarrow {S_{A'B'C'D'}} = \frac{{12}}{4} = 3\left( {c{m^2}} \right)\)
Trong các cặp tam giác sau cặp tam giác nào đồng dạng nếu các cạnh của hai tam giác có độ dài là :
-
A.
\(3cm;4cm;6cm\) và \(9cm;15cm;18cm\) .
-
B.
\(4cm;5cm;6cm\) và \(8cm;10cm;12cm\) .
-
C.
\(6cm;5cm;6cm\) và \(3cm;5cm;3cm\) .
-
D.
\(5cm;7cm;1dm\) và \(10cm;14cm;18cm\) .
Đáp án : B
Vì \(\frac{3}{8} = \frac{6}{{18}}\left( { = \frac{1}{2}} \right) \ne \frac{4}{{15}}\) nên hai tam giác có độ dài các cạnh 3cm; 4cm; 6cm và 9 cm; 15cm; 18 cm không đồng dạng với nhau
Vì \(\frac{4}{8} = \frac{5}{{10}} = \frac{6}{{12}}\) nên hai tam giác có độ dài các cạnh là 4cm; 5cm; 6cm và 8cm; 10cm; 12cm đồng dạng với nhau theo trường hợp thứ nhất. Chọn B
Vì \(\frac{6}{3} = \frac{6}{3} \ne \frac{5}{5}\) nên hai tam giác có độ dài các cạnh là 6cm; 5 cm; 6 cm và 3cm; 5cm; 3 cm không đồng dạng với nhau.
Vì \(\frac{5}{{10}} = \frac{7}{{14}} \ne \frac{{10}}{{18}}\) nên hai tam giác có độ dài các cạnh là 5cm; 7cm; 1 dm và 10cm; 14cm; 18 cm không đồng dạng với nhau.
Cho tam giác ABC có AB = 6cm; AC = 9cm; BC = 12cm và tam giác MNP có NP = 8cm; MN= 12cm; PM = 16cm. khẳng định nào sau đây là đúng?
-
A.
\(\Delta ABC \backsim \Delta MNP\)
-
B.
\(\Delta ABC \backsim \Delta NMP\)
-
C.
\(\Delta ABC \backsim \Delta NPM\)
-
D.
\(\Delta BAC \backsim \Delta MNP\)
Đáp án : C
Vì \(\frac{{AB}}{{NP}} = \frac{6}{8} = \frac{3}{4};\frac{{AC}}{{NM}} = \frac{9}{{12}} = \frac{3}{4};\frac{{BC}}{{PM}} = \frac{{12}}{{16}} = \frac{3}{4}\)
Nên \(\frac{{AB}}{{NP}} = \frac{{AC}}{{NM}} = \frac{{BC}}{{PM}} = \frac{3}{4} \Rightarrow \Delta ABC \backsim \Delta NPM\)
Với điều kiện nào sau đây thì \(\Delta ABC \backsim \Delta MNP\)
-
A.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\) .
-
B.
\(\frac{{AB}}{{MP}} = \frac{{AC}}{{MN}} = \frac{{BC}}{{NP}}\) .
-
C.
\(\frac{{AB}}{{NP}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{MN}}\) .
-
D.
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{NP}} = \frac{{BC}}{{MP}}\) .
Đáp án : A
\(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} \Rightarrow \Delta ABC \backsim \Delta MNP\)
Cho \(\Delta ABC \backsim \Delta MNP\) biết \(AB = 3cm;BC = 4cm;MN = 6cm;MP = 5cm\) . Khi đó:
-
A.
AC = 8cm; NP = 2,5cm
-
B.
AC = 2,5cm; NP = 8cm
-
C.
AC = 2,5cm; NP = 10cm
-
D.
AC = 10cm; NP = 2cm
Đáp án : B
\(\begin{array}{l}\Delta ABC \backsim \Delta MNP\\ \Rightarrow \frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}}\\ \Rightarrow \frac{3}{6} = \frac{{AC}}{5} = \frac{4}{{NP}}\\ \Rightarrow AC = \frac{{3.5}}{6} = 2,5(cm)\\ \Rightarrow NP = \frac{{4.6}}{3} = 8(cm)\end{array}\)
Vậy AC = 2,5cm; NP = 8cm
Cho tam giác ABC có AB = 3cm, AC = 5cm; BC = 7cm và MNP có MN = 6cm;
MP = 10cm; NP = 14cm. Tỉ số chu vi của hai tam giác ABC và MNP là
-
A.
\(\frac{3}{5}\) .
-
B.
2.
-
C.
\(\frac{5}{6}\) .
-
D.
\(\frac{1}{2}\) .
Đáp án : D
Vì \(\frac{{AB}}{{MN}} = \frac{3}{6} = \frac{1}{2};\frac{{AC}}{{MP}} = \frac{5}{{10}} = \frac{1}{2};\frac{{BC}}{{NP}} = \frac{7}{{14}} = \frac{1}{2}\)
Suy ra: \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} = \frac{1}{2} \Rightarrow \Delta ABC \backsim \Delta MNP\) theo tỉ số đồng dạng là \(\frac{1}{2}\)
Vì \(\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}} = \frac{{BC}}{{NP}} = \frac{{AB + AC + BC}}{{MN + MP + NP}} = \frac{1}{2}\)
\( \Rightarrow \frac{{C{V_{\Delta ABC}}}}{{C{V_{\Delta MNP}}}} = \frac{1}{2}\)
Cho hai tam giác ABC và DEF có kích thước như trong hình, hai tam giác có đồng dạng với nhau không, nếu có thì tỉ số đồng dạng là bao nhiêu?

-
A.
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) tỉ số đồng dạng là 2.
-
B.
Hai tam giác không đồng dạng.
-
C.
\(\Delta ABC \backsim \Delta {\rm{FED}}\) tỉ số đồng dạng là \(\frac{5}{3}\) .
-
D.
\(\Delta ABC \backsim \Delta D{\rm{EF}}\) tỉ số đồng dạng là \(\frac{5}{3}\) .
Đáp án : D
Vì \(\frac{{AB}}{{DE}} = \frac{5}{3};\frac{{AC}}{{DF}} = \frac{{7,5}}{{4,5}} = \frac{5}{3};\frac{{BC}}{{EF}} = \frac{{10}}{6} = \frac{5}{3}\)
Suy ra: \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{5}{3} \Rightarrow \Delta ABC \backsim \Delta DEF\) với tỉ số đồng dạng là \(\frac{5}{3}\)
Tỉ số của các cạnh tương ứng là tỉ số đồng dạng của hai tam giác.
-
A.
\(\Delta ABC \backsim \Delta DBC\)
-
B.
\(\Delta A{\rm{D}}B \backsim \Delta DBC\)
-
C.
\(\Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C\)
-
D.
\(\Delta A{\rm{D}}C \backsim \Delta ABC\)
Đáp án : B
Vì \(\frac{{AD}}{{DB}} = \frac{4}{8} = \frac{1}{2};\frac{{AB}}{{DC}} = \frac{6}{{12}} = \frac{1}{2};\frac{{B{\rm{D}}}}{{BC}} = \frac{8}{{16}} = \frac{1}{2}\)
Suy ra: \(\frac{{AD}}{{DB}} = \frac{{AB}}{{DC}} = \frac{{DB}}{{BC}} = \frac{1}{2} \Rightarrow \Delta A{\rm{D}}B \backsim \Delta DBC\) (Trường hợp đồng dạng thứ nhất),
Cho tam giác ABC có AB = 3cm; AC = 6cm; BC = 9cm và MNP có MN = 1cm; MP = 2cm; NP = 3cm. Tỉ số chu vi của hai tam giác MNP và ABC là
-
A.
\(\frac{1}{2}\) .
-
B.
3.
-
C.
\(\frac{1}{3}\) .
-
D.
2.
Đáp án : C
Vì \(\frac{{MN}}{{AB}} = \frac{1}{3};\frac{{MP}}{{AC}} = \frac{2}{6} = \frac{1}{3};\frac{{NP}}{{BC}} = \frac{3}{9} = \frac{1}{3}\)
Suy ra: \(\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}} = \frac{1}{3}\)
Do đó \(\Delta MNP \backsim \Delta ABC\) theo tỉ số đồng dạng \(\frac{1}{3}\) .
Vì \(\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}}\) nên áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}} = \frac{{MN + MP + NP}}{{AB + AC + BC}} = \frac{{C{V_{\Delta MNP}}}}{{C{V_{\Delta ABC}}}} = \frac{1}{3}\)
Cho \(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) khẳng định nào sau đây là sai
-
A.
\(\frac{{AB}}{{{A_1}{B_1}}} = \frac{{AC}}{{{A_1}{C_1}}} = \frac{{BC}}{{{B_1}{C_1}}}\) .
-
B.
\(\frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}}\) .
-
C.
\(\frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{A_1}{B_1}}}{{AB}}\) .
-
D.
\(\frac{{AB}}{{{A_1}{B_1}}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{BC}}{{{B_1}{C_1}}}\) .
Đáp án : D
\(\Delta ABC \backsim \Delta {A_1}{B_1}{C_1}\) \( \Rightarrow \frac{{AB}}{{{A_1}{B_1}}} = \frac{{AC}}{{{A_1}{C_1}}} = \frac{{BC}}{{{B_1}{C_1}}}\) (các cạnh tương ứng)
\( \Rightarrow \frac{{{A_1}{B_1}}}{{AB}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{B_1}{C_1}}}{{BC}}\) (Tính chất tỉ lệ thức)
\( \Rightarrow \frac{{{B_1}{C_1}}}{{BC}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{{A_1}{B_1}}}{{AB}}\) (Tính chất tỉ lệ thức)
\( \Rightarrow \frac{{AB}}{{{A_1}{B_1}}} = \frac{{{A_1}{C_1}}}{{AC}} = \frac{{BC}}{{{B_1}{C_1}}}\) là khẳng định sai
Cho tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với \(4:5:6\) . Cho biết \(\Delta ABC \backsim \Delta A'B'C'\) và cạnh nhỏ nhất của \(\Delta A'B'C'\) bằng 2cm. Độ dài các cạnh còn lại của tam giác \(A'B'C'\) lần lượt là
-
A.
3cm; 4cm
-
B.
2,5cm; 4cm.
-
C.
3cm; 2cm
-
D.
2,5cm; 3cm.
Đáp án : D
Theo đầu bài tam giác ABC có độ dài các cạnh lần lượt tỉ lệ với \(4:5:6\)
Và \(\Delta ABC \backsim \Delta A'B'C'\) nên \(\Delta A'B'C'\) cũng có độ dài các cạnh tỉ lệ với \(4:5:6\)
Giả sử \(A'B' < A'C' < B'C' \Rightarrow A'B' = 2cm\)
\( \Rightarrow \frac{{A'B'}}{4} = \frac{{A'C'}}{5} = \frac{{B'C'}}{6} \Rightarrow \frac{{A'C'}}{5} = \frac{{B'C'}}{6} = \frac{2}{4}\)
\(\begin{array}{l} \Rightarrow A'C' = \frac{{5.2}}{4} = 2,5(cm)\\ \Rightarrow B'C' = \frac{{6.2}}{4} = 3(cm)\end{array}\)
Độ dài các cạnh còn lại của tam giác A’B’C’ lần lượt là 2,5cm ; 3cm.
Tam giác thứ nhất có cạnh nhỏ nhất bằng 8cm, hai cạnh còn lại bằng x và y (x < y). Tam giác thứ hai có cạnh lớn nhất bằng 27cm hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đồng dạng:
-
A.
x = 12cm; y = 18cm
-
B.
x = 9cm; y = 24cm
-
C.
x = 18cm; y = 12cm
-
D.
x = 8cm; y = 27cm
Đáp án : A
Theo đề bài:
Tam giác thứ nhất có cạnh lần lượt là 8; x; y (8 < x < y)
Tam giác thứ hai có cạnh lần lượt là x; y ; 27 ( x < y < 27)
Để hai tam giác đồng dạng cần:
\(\begin{array}{l}\frac{8}{x} = \frac{x}{y} = \frac{y}{{27}}\\ \Rightarrow xy = 8.27;{x^2} = 8y\\ \Rightarrow y = \frac{{8.27}}{x};{x^2} = 8.\frac{{8.27}}{x} \Rightarrow {x^3} = 64.27 = {\left( {4.3} \right)^3}\end{array}\)
Vậy x = 12cm; y = 18cm
Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Cho biết tam giác ABC có chu vi bằng 450cm, chu vi tam giác PQR có độ dài là
-
A.
220cm
-
B.
900cm
-
C.
225cm
-
D.
150cm
Đáp án : C
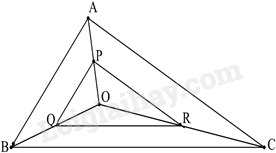
Vì P, Q, R lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Nên PQ, QR, RP lần lượt là đường trung bình của các tam giác AOB; BOC; AOC. Nên ta có:
\(\frac{{PQ}}{{AB}} = \frac{{Q{\rm{R}}}}{{BC}} = \frac{{P{\rm{R}}}}{{AC}} = \frac{1}{2}\)
Suy ra: \(\Delta PQ{\rm{R}} \backsim \Delta ABC\)
Vì:
\(\begin{array}{l}\frac{{PQ}}{{AB}} = \frac{{Q{\rm{R}}}}{{BC}} = \frac{{P{\rm{R}}}}{{AC}} = \frac{{PQ + Q{\rm{R}} + P{\rm{R}}}}{{AB + BC + AC}} = \frac{{C{V_{\Delta PQ{\rm{R}}}}}}{{C{V_{\Delta ABC}}}}\\ \Rightarrow \frac{{C{V_{\Delta PQ{\rm{R}}}}}}{{C{V_{\Delta ABC}}}} = \frac{1}{2} \Rightarrow C{V_{\Delta PQ{\rm{R}}}} = \frac{{C{V_{\Delta ABC}}}}{2} = \frac{{450}}{2} = 225(cm)\end{array}\)
Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm và tam giác A’B’C’ vuông tại A’ có A’B’= 3cm; A’C’ = 4cm. Tam giác ABC đồng dạng với tam giác A’B’C’ không và nếu có thì tỉ số chu vi của hai tam giác là bao nhiêu?
-
A.
\(\Delta ABC \backsim \Delta A'B'C'\) tỉ số chu vi của hai tam giác là 2.
-
B.
Hai tam giác không đồng dạng.
-
C.
\(\Delta ABC \backsim \Delta A'B'C'\) tỉ số chu vi của hai tam giác là 3.
-
D.
\(\Delta ABC \backsim \Delta A'B'C'\) tỉ số chu vi của hai tam giác là \(\frac{3}{2}\) .
Đáp án : A
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:
\(A{B^2} + A{C^2} = B{C^2} \Rightarrow B{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = 10(cm)\)
Áp dụng định lý Pythagore vào tam giác A’B’C’ vuông tại A’ ta có:
\(A'B{'^2} + A'C{'^2} = B'C{'^2} \Rightarrow B'C{'^2} = {3^2} + {4^2} = 25 \Rightarrow B'C' = 5(cm)\)
Ta thấy: \(\frac{{AB}}{{A'B'}} = \frac{6}{3} = 2;\frac{{AC}}{{A'C'}} = \frac{8}{4} = 2;\frac{{BC}}{{B'C'}} = \frac{{10}}{5} = 2\)
\( \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}} = \frac{{C{V_{\Delta ABC}}}}{{C{V_{\Delta A'B'C'}}}} = 2\)
Vì \(\Delta ABC \backsim \Delta A'B'C'\) tỉ số chu vi của hai tam giác là 2.
Luyện tập và củng cố kiến thức Bài 7: Trường hợp đồng dạng thứ hai của tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Trường hợp đồng dạng thứ ba của tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 9: Hình đồng dạng Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 10: Hình đồng dạng trong thực tiễn Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Tam giác đồng dạng Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Tính chất đường phân giác của tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Đường trung bình của tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Ứng dụng của định lí Thalès trong tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Định lí Thalès trong tam giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 10: Hình đồng dạng trong thực tiễn Toán 8 Cánh diều
- Trắc nghiệm Bài 9: Hình đồng dạng Toán 8 Cánh diều
- Trắc nghiệm Bài 8: Trường hợp đồng dạng thứ ba của tam giác Toán 8 Cánh diều
- Trắc nghiệm Bài 7: Trường hợp đồng dạng thứ hai của tam giác Toán 8 Cánh diều
- Trắc nghiệm Bài 6: Trường hợp đồng dạng thứ nhất của tam giác Toán 8 Cánh diều











Danh sách bình luận