-
Giải Toán 12 tập 1 - Cánh diều
-
Giải Toán 12 tập 2 - Cánh diều
Lý thuyết Xác suất có điều kiện Toán 12 Cánh Diều
1. Định nghĩa xác suất có điều kiện
Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa
1. Định nghĩa xác suất có điều kiện
|
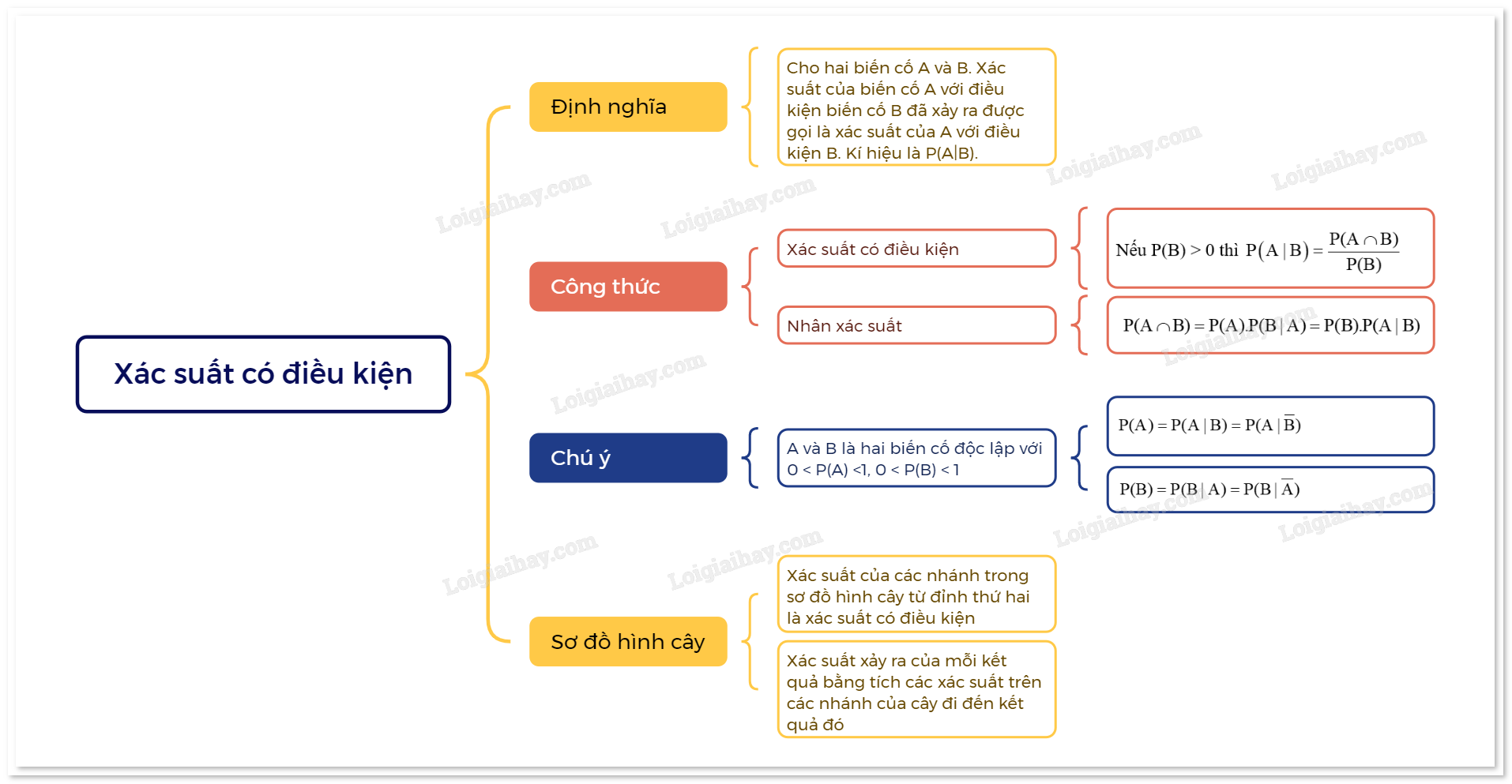
Cho hai biến cố A và B. Xác suất của biến cố A với điều kiện biến cố B đã xảy ra được gọi là xác suất của A với điều kiện B. Kí hiệu là P(A|B). Nếu P(B) > 0 thì \(P\left( {A|B} \right) = \frac{{P(A \cap B)}}{{P(B)}}\). |
Nhận xét:
- Từ định nghĩa của xác suất có điều kiện, ta suy ra: Nếu P(B) > 0 thì
\(P(A \cap B) = P(B).P(A|B)\)
- Người ta chứng minh được rằng: Nếu A, B là hai biến cố bất kì thì
\(P(A \cap B) = P(A).P(B|A) = P(B).P(A|B)\)
Công thức trên gọi là công thức nhân xác suất.
Ví dụ 1: Cho hai biến cố A, B có P(A) = 0,4; P(B) = 0,6; \(P(A \cap B) = 0,2\). Tính các xác suất sau: \(P(A|B)\); \(P(B|A)\).
Giải:
Ta có: \(P(A|B) = \frac{{P(A \cap B)}}{{P(B)}} = \frac{{0,2}}{{0,6}} = \frac{1}{3}\); \(P(B|A) = \frac{{P(B \cap A)}}{{P(A)}} = \frac{{0,2}}{{0,4}} = 0,5\).
Ví dụ 2: Trong kỳ kiểm tra môn Toán của một trường trung học phổ thông có 200 học sinh tham gia, trong đó có 95 học sinh nam và 105 học sinh nữ. Khi công bố kết quả của kỳ kiểm tra đó, có 50 học sinh đạt điểm giỏi, trong đó có 24 học sinh nam và 26 học sinh nữ. Chọn ra ngẫu nhiên một học sinh trong số 200 học sinh đó. Tính xác suất để học sinh được chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ (làm tròn kết quả đến hàng phần trăm).
Giải:
Xét hai biến cố sau:
A: "Học sinh được chọn ra đạt điểm giỏi".
B: "Học sinh được chọn ra là học sinh nữ".
Khi đó, xác suất để học sinh được chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ, chính là xác suất của A với điều kiện B.
Do có 26 học sinh nữ đạt điểm giỏi nên \(P(A \cap B) = \frac{{26}}{{200}} = 0,13\).
Do có 105 học sinh nữ nên \(P(B) = \frac{{105}}{{200}} = 0,525\). Vì thế, ta có:
\(P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{0,13}}{{0,525}} \approx 0,25\).
Vì thế, ta có:
Vậy xác suất để học sinh được chọn ra đạt điểm giỏi, biết rằng học sinh đó là nữ, là 0,25.
Ví dụ 3: Một công ty dược phẩm giới thiệu một dụng cụ kiểm tra sớm bệnh sốt xuất huyết. Về kiểm định chất lượng của sản phẩm, họ cho biết như sau: Số người được thử là 9000, trong số đó có 1500 người đã bị nhiễm bệnh sốt xuất huyết và có 7500 người không bị nhiễm bệnh sốt xuất huyết. Khi thử bằng dụng cụ của công ty, trong 1500 người đã bị nhiễm bệnh sốt xuất huyết, có 76% số người đó cho kết quả dương tính, còn lại cho kết quả âm tính. Mặt khác, trong 7500 người không bị nhiễm bệnh sốt xuất huyết, có 7% số người đó cho kết quả dương tính, còn lại cho kết quả âm tính khi kiểm tra.
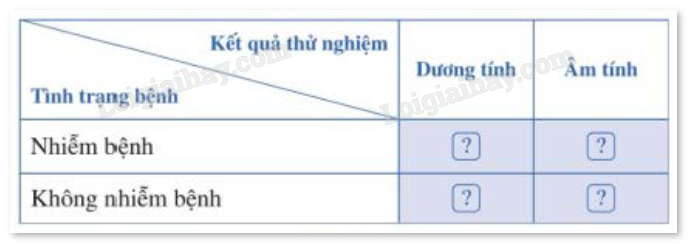
a) Chọn số thích hợp cho (?) trong bảng (đơn vị: người). So sánh số người có kết quả dương tính khi thử nghiệm với số người bị nhiễm bệnh sốt xuất huyết.
b) Chọn ngẫu nhiên một người trong số những người thử nghiệm. Tính xác suất để người được chọn ra bị nhiễm bệnh sốt xuất huyết, biết rằng người đó có kết quả thử nghiệm dương tính (làm tròn kết quả đến hàng phần mười).
c) Nhà sản xuất khẳng định dung cụ cho kết quả dương tính với hơn 90% số trường hợp có kết quả dương tính. Khẳng định đó có đúng không?
Giải:
a) Trong 1500 người đã bị nhiễm bệnh sốt xuất huyết, số người cho kết quả dương tính (khi kiểm tra) là: 76%.1500 = 1140 (người).
Trong 1500 người đã bị nhiễm bệnh sốt xuất huyết, số người cho kết quả âm tính (khi kiểm tra) là: 1500 − 1140 = 360 (người).
Trong 7500 người không bị nhiễm bệnh sốt xuất huyết, số người cho kết quả dương tính (khi kiểm tra) là: 7%.7500 = 525 (người).
Do đó, số người không bị nhiễm bệnh sốt xuất huyết cho kết quả âm tính (khi kiểm tra) là: 7500 – 525 = 6975 (người).
Từ đó, bảng được hoàn thiện.
Từ bảng ta thấy số người có kết quả dương tính khi thử nghiệm là 525 + 1140 = 1665 > 1500.
b) Xét các biến cố sau:
A: "Người được chọn ra trong số những người thử nghiệm là bị nhiễm bệnh sốt xuất huyết";
B: "Người được chọn ra trong số những người thử nghiệm cho kết quả dương tính (khi kiểm tra)".
Từ các dữ liệu thống kê ở bảng, ta có:
\(P(B) = \frac{{1665}}{{9000}} = \frac{{37}}{{200}}\); \(P(A \cap B) = \frac{{1140}}{{9000}} = \frac{{19}}{{150}}\).
Vậy \(P(A|B) = \frac{{19}}{{150}}:\frac{{37}}{{200}} = \frac{{76}}{{111}} \approx 68,5\% \).
c) Do 68,5% < 90% nên khẳng định của nhà sản xuất là không đúng.
Chú ý: Người ta chứng minh được tính chất sau chỉ ra mối liên hệ giữa xác suất có điều kiện và biến cố độc lập: Cho A và B là hai biến cố với 0 < P(A) <1, 0 < P(B) < 1. Khi đó, A và B là hai biến cố độc lập khi và chỉ khi \(P(A) = P(A|B) = P(A|\overline B )\) và \(P(B) = P(B|A) = P(B|\overline A )\).
Nhận xét: Tính chất trên giải thích vì sao hai biến cố là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng đến xác suất xảy ra của biến cố kia.
2. Sử dụng sơ đồ hình cây để tính xác suất có điều kiện
Ví dụ: Giả sử có 8 viên bi màu đỏ và 5 viên bi màu vàng trong một hộp. Từ 13 viên bi này, 5 viên bi được đánh số, trong đó có 3 viên bi màu đỏ. Ta cần tìm xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó được đánh số.
Giải:
Xét hai biến cố sau:
A: “Viên bi được lấy ra có màu đỏ”.
B: “Viên bi được lấy ra có đánh số”.
Khi đó, xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó được đánh số, chính là xác suất có điều kiện P(A∣B).
Sơ đồ hình cây biểu thị cách tính xác suất có điều kiện P(A∣B), được vẽ như sau:
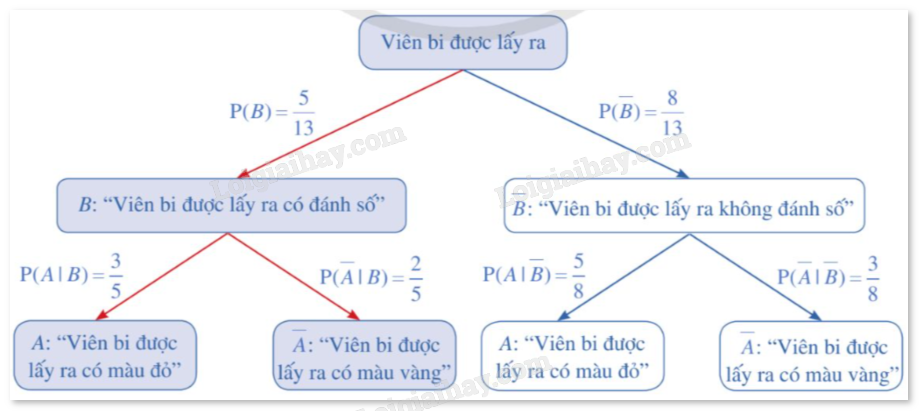
Vậy xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó có đánh số là 0,6.
Ta có thể tính \(P\left( {A|B} \right) = \frac{{n(AB)}}{{N(B)}} = \frac{3}{5} = 0,6\).
Nhận xét:
- Xác suất của các nhánh trong sơ đồ hình cây từ đỉnh thứ hai là xác suất có điều kiện.
- Xác suất xảy ra của mỗi kết quả bằng tích các xác suất trên các nhánh của cây đi đến kết quả đó.
Bình luận
Chia sẻ
- Giải mục 1 trang 90, 91, 92, 93, 94 SGK Toán 12 tập 2 - Cánh diều
- Giải mục 2 trang 94, 95 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 1 trang 95 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 2 trang 95 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 3 trang 95 SGK Toán 12 tập 2 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Cánh diều - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
