Lý thuyết về mặt phẳng toạ độ
1. Mặt phẳng toạ độ
1. Mặt phẳng toạ độ
Trên mặt phẳng, nếu hai trục \(Ox, Oy\) vuông góc và cắt nhau tại gốc \(O\) của mỗi trục số, thì ta gọi đó là hệ trục toạ độ \(Oxy.\)
\(Ox\) và \(Oy\) gọi là các trục toạ độ
- Trục nằm ngang \(Ox\) gọi là trục hoành.
- Trục thẳng đứng \(Oy\) gọi là trục tung.
Giao điểm \(O\) gọi là gốc toạ độ. Mặt phẳng có hệ trục toạ độ \(Oxy\) gọi là mặt phẳng toạ độ \(Oxy.\)
2. Toạ độ của một điểm trong mặt phẳng toạ độ
- Trên mặt phẳng toạ độ, mỗi điểm \(M\) xác định một cặp số \(({x_0};{y_0})\). Ngược lại mỗi cặp số \(({x_0};{y_0})\) xác định vị trí của một điểm \(M.\)
- Cặp số \(({x_0};{y_0})\) gọi là toạ độ của điểm \(M\); \({x_0}\) là hoành độ và \({y_0}\) là tung độ của điểm \(M.\)
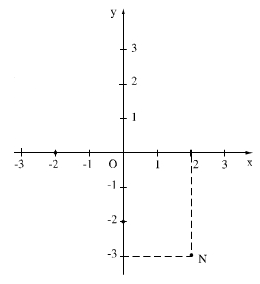
Ví dụ: Trên hình vẽ ta có \(N(2;-3)\) với x=2 là hoành độ và y=-3 là tung độ của N.
Chú ý: Các điểm nằm trên trục hoành có tung độ bằng 0
Các điểm nằm trên trục tung có hoành độ bằng 0
Bình luận
Chia sẻ
- Trả lời câu hỏi 1 Bài 6 trang 66 SGK Toán 7 Tập 1
- Trả lời câu hỏi 2 Bài 6 trang 67 SGK Toán 7 Tập 1
- Bài 32 trang 67 SGK Toán 7 tập 1
- Bài 33 trang 67 SGK Toán 7 tập 1
- Bài 34 trang 68 SGK Toán 7 tập 1
>> Xem thêm
Tham Gia Group Dành Cho Lớp 7 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
