Bài 35 trang 68 SGK Toán 7 tập 1
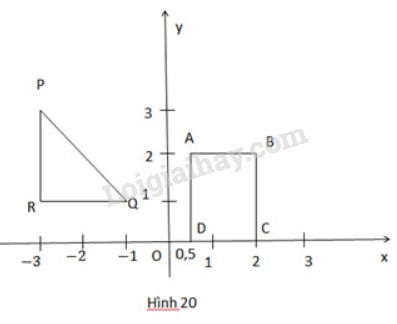
Tìm tọa độ các đỉnh của hình chữ nhật ABCD và của hình tam giác PQR trong hình 20.
Đề bài
Tìm tọa độ các đỉnh của hình chữ nhật \(ABCD\) và của hình tam giác \(PQR\) trong hình \(20.\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Từ điểm cần xác định tọa độ ta vẽ các đường vuông góc với các trục tọa độ, xác định giao điểm của các đường này với các trục tọa độ từ đó ta tìm được tọa độ của điểm cần xác định.
Lời giải chi tiết
Từ các đỉnh của hình chữ nhật \(ABCD\) và các đỉnh của hình tam giác \(PQR\) ta vẽ các đường vuông góc xuống các trục \(Ox\) và \(Oy\).
Tọa độ giao điểm của các đường vuông góc với \(Ox\) và \(Oy\) cho ta biết hoành độ và tung độ của điểm đó. Vậy tọa độ các đỉnh của hình chữ nhật \(ABCD\) là
\(A (0,5; 2)\); \(B (2;2)\); \(C (2;0)\); \(D (0,5; 0)\).
Tọa độ các đỉnh của hình \(\Delta PQR\) là:
\(P (-3;3)\); \(Q (-1;1)\); \(R(-3;1)\).
Loigiaihay.com













Danh sách bình luận