-
Toán 9 tập 1 - Cánh diều
-
Toán 9 tập 2 - Cánh diều
Lý thuyết Tứ giác nội tiếp đường tròn Toán 9 Cánh diều
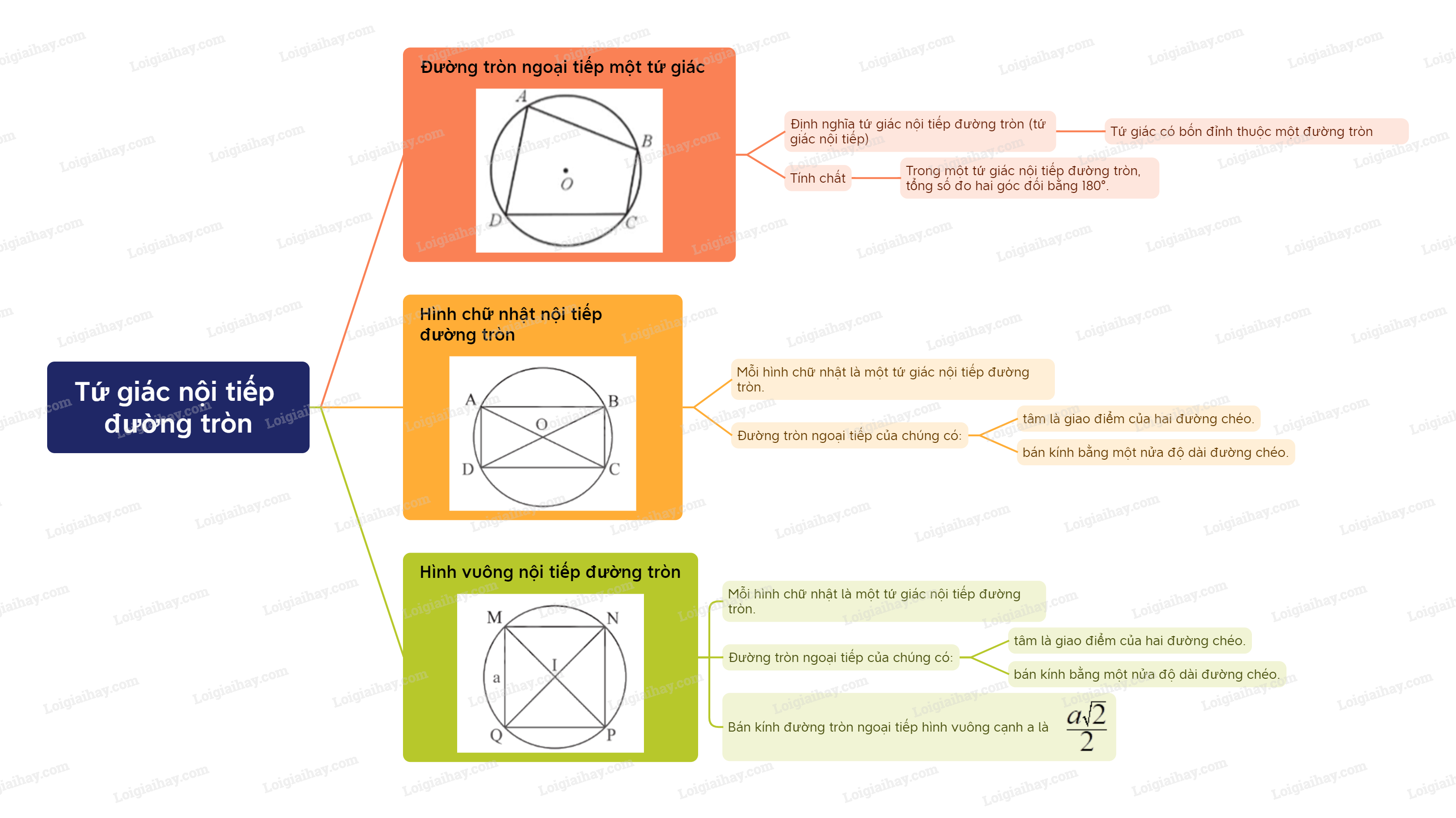
1. Đường tròn ngoại tiếp của một tứ giác Định nghĩa đường tròn ngoại tiếp tứ giác Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay còn gọi là tứ giác nội tiếp).
Tổng hợp đề thi giữa kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
1. Đường tròn ngoại tiếp của một tứ giác
Định nghĩa đường tròn ngoại tiếp tứ giác
|
Tứ giác có bốn đỉnh thuộc một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay còn gọi là tứ giác nội tiếp). |
Ví dụ:
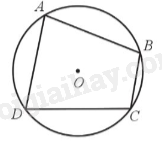
Tứ giác ABCD là tứ giác nội tiếp và đường tròn (O) được gọi là đường tròn ngoại tiếp tứ giác ABCD.
Tính chất
|
Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng \(180^\circ \). |
Ví dụ:
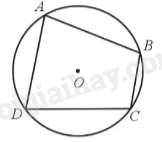
Tứ giác ABCD nội tiếp (O) nên \(\widehat A + \widehat C = 180^\circ ;\widehat B + \widehat D = 180^\circ \).
2. Hình chữ nhật, hình vuông nội tiếp đường tròn
Hình chữ nhật nội tiếp đường tròn
|
- Mỗi hình chữ nhật là một tứ giác nội tiếp đường tròn. - Tâm của đường tròn ngoại tiếp hình chữ nhật là giao điểm của hai đường chéo và mỗi đường chéo là một đường kính của đường tròn đó.
|
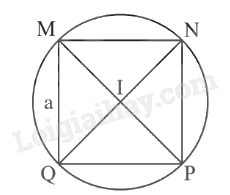
Hình vuông nội tiếp đường tròn
|
- Mỗi hình vuông là một tứ giác nội tiếp đường tròn. - Tâm của đường tròn ngoại tiếp hình vuông là giao điểm của hai đường chéo và mỗi đường chéo là một đường kính của đường tròn. Bán kính của đường tròn ngoại tiếp hình vuông cạnh a là \(\frac{{a\sqrt 2 }}{2}\).
|
Ví dụ:
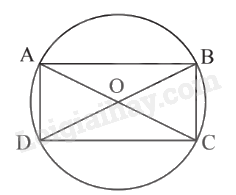
Áp dụng định lí Pythagore cho tam giác ABD vuông tại A, ta có:
\(B{D^2} = A{B^2} + A{D^2} = {3^2} + {4^2} = 25\) nên \(BD = 5cm\).
Do đó, ta có \(R = \frac{{BD}}{2} = 2,5cm\).
Đường tròn (O;2,5) là đường tròn ngoại tiếp hình chữ nhật ABCD.
Bình luận
Chia sẻ
- Giải mục 1 trang 75 SGK Toán 9 tập 2 - Cánh diều
- Giải mục 2 trang 76 SGK Toán 9 tập 2 - Cánh diều
- Giải mục 3 trang 76, 77 SGK Toán 9 tập 2 - Cánh diều
- Giải bài tập 1 trang 78 SGK Toán 9 tập 2 - Cánh diều
- Giải bài tập 2 trang 78 SGK Toán 9 tập 2 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
