Lý thuyết Lũy thừa - SGK Toán 11 Cùng khám phá
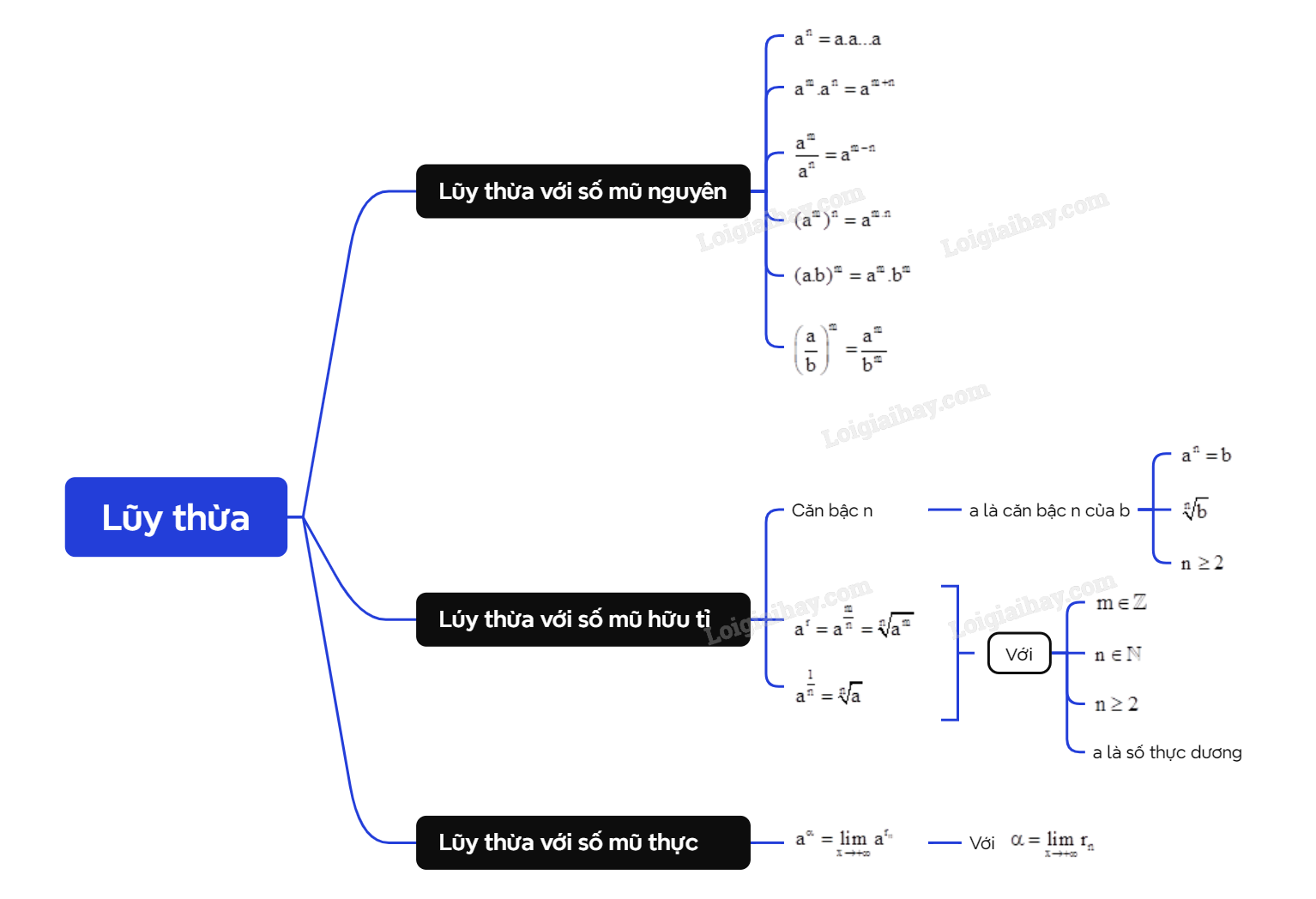
A. Lý thuyết 1. Lũy thừa với số mũ nguyên
A. Lý thuyết
1. Lũy thừa với số mũ nguyên
|
Cho n là một số nguyên dương. - Với a là số thực tùy ý, lũy thừa bậc n của a là tích của n thừa số a. \({a^n} = a.a...a\) (n thừa số a). - Với \(a \ne 0\): \({a^{ - n}} = \frac{1}{{{a^n}}}\). |
Trong biểu thức \({a^n}\), ta gọi a là cơ số, số nguyên n là số mũ.
Lưu ý:
- Với \(a \ne 0\) thì \({a^0} = 1\).
- \({0^0}\) với \({0^{ - n}}\) với \(n \in \mathbb{N}\) không có nghĩa.
|
Cho a, b là các số thực khác 0 và với các số nguyên m, n, ta có: +) \({a^m}.{a^n} = {a^{m + n}}\) +) \(\frac{{{a^m}}}{{{a^n}}} = {a^{m - n}}\) +) \({({a^m})^n} = {a^{m.n}}\) +) \({(a.b)^m} = {a^m}.{b^m}\) +) \({\left( {\frac{a}{b}} \right)^m} = \frac{{{a^m}}}{{{b^m}}}\) |
2. Lúy thừa với số mũ hữu tỉ
| Cho số thực b và số nguyên dương n \((n \ge 2)\). Số a được gọi là căn bậc n của số b nếu \({a^n} = b\). |
Lưu ý:
- Với n lẻ và \(b \in \mathbb{R}\), có duy nhất một căn bậc n của b, kí hiệu là \(\sqrt[n]{b}\).
- Với n chẵn và:
+ b < 0: Không tồn tại căn bậc n của b.
+ b = 0: Có một căn bậc n của b là số 0.
+ b > 0: Có hai căn bậc n trái dấu, giá trị dương kí hiệu là \(\sqrt[n]{b}\) và giá trị âm kí hiệu là \( - \sqrt[n]{b}\).
|
Cho số thực a dương và số hữu tỉ \(r = \frac{m}{n}\), trong đó \(m \in \mathbb{Z}\), \(n \in \mathbb{N}\), \(n \ge 2\). Lũy thừa của số a với số mũ r, kí hiệu \({a^r}\) xác định bởi: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\). |
Lưu ý : \({a^{\frac{1}{n}}} = \sqrt[n]{a}\) với a > 0 và \(n \in \mathbb{N}\), \(n \ge 2\).
| Lũy thừa với số mũ hữu tỉ của số thực dương có đầy đủ các tính chất như lũy thừa với số mũ nguyên. |
3. Lũy thừa với số mũ thực
|
Cho số thực a dương và số vô tỉ \(\alpha \), trong đó \(\alpha = \mathop {\lim }\limits_{x \to + \infty } {r_n}\) với \(({r_n})\) là một dãy số hữu tỉ. Giới hạn của dãy số \(({a^{{r_n}}})\) gọi là lũy thừa của số a với số mũ \(\alpha \), kí hiệu \({a^\alpha }\). \({a^\alpha } = \mathop {\lim }\limits_{x \to + \infty } {a^{{r_n}}}\) với \(\alpha = \mathop {\lim }\limits_{x \to + \infty } {r_n}\). |
Lưu ý:
- Từ định nghĩa, ta có \({1^\alpha } = 1\) \((\alpha \in \mathbb{R})\).
- Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số khác 0.
- Khi xét lũy thừa với số mũ không nguyên thì cơ số phải dương.
| Lũy thừa với số mũ thực dương có các tính chất tương tự lũy thừa vơi số mũ nguyên. |
B. Bài tập
Bài 1:
a) Không dùng máy tính cầm tay, rút gọn giá trị biểu thức:
\(A = {\left( {\frac{1}{3}} \right)^{ - 10}}{.27^{ - 3}} + {(0,2)^{ - 4}}{.25^{ - 2}}{.128^{ - 1}}.{\left( {\frac{1}{2}} \right)^{ - 9}}\).
b) Rút gọn biểu thức: \(B = \left[ {\frac{{a\sqrt 2 }}{{{{(1 + {a^2})}^{ - 1}}}} - \frac{{2\sqrt 2 }}{{{a^{ - 1}}}}} \right].\frac{{{a^{ - 1}}}}{{1 - {a^{ - 2}}}}\) \((a \ne 0,a \ne 1,a \ne - 1)\).
Giải:
a) \(A = {({3^{ - 1}})^{ - 10}}.{({3^3})^{ - 3}} + {({5^{ - 1}})^{ - 4}}.{({5^2})^{ - 2}} + {({2^7})^{ - 1}}.{({2^{ - 1}})^{ - 9}}\)
\( = {3^{10}}{.3^{ - 9}} + {5^4}{.5^{ - 4}} + {2^{ - 7}}{.2^9}\)
\( = {3^1} + {5^0} + {2^2} = 8\).
b) \(B = \left[ {a\sqrt 2 (1 + {a^2}) - 2\sqrt 2 a} \right].\frac{1}{{{a^3}(1 - {a^{ - 2}})}}\)
\( = (a\sqrt 2 + {a^3}\sqrt 2 - 2a\sqrt 2 ).\frac{1}{{{a^3} - a}}\)
\( = a\sqrt 2 ({a^2} - 1).\frac{1}{{a({a^2} - 1)}} = \sqrt 2 \).
Bài 2:
a) Không dùng máy tính cầm tay, tính giá trị biểu thức \(A = {\left( {\frac{1}{{27}}} \right)^{\frac{1}{3}}} + {9^{ - \frac{3}{2}}}\).
b) Rút gọn biểu thức \(C = \frac{{{x^{\frac{6}{5}}}y + x{y^{\frac{6}{5}}}}}{{\sqrt[5]{x} + \sqrt[5]{y}}}\) (x > 0, y > 0).
Giải:
a) Ta có \({\left( {\frac{1}{{27}}} \right)^{\frac{1}{3}}} = \sqrt[3]{{\frac{1}{{27}}}} = \frac{1}{3}\); \({9^{ - \frac{3}{2}}} = \sqrt {{9^{ - 3}}} = \sqrt {\frac{1}{{{9^3}}}} = {\left( {\sqrt {\frac{1}{9}} } \right)^3} = \frac{1}{{27}}\).
Vậy \(A = {\left( {\frac{1}{{27}}} \right)^{\frac{1}{3}}} + {9^{ - \frac{3}{2}}} = \frac{1}{3} + \frac{1}{{27}} = \frac{{10}}{{27}}\).
b) Với x, y là các số dương, theo định nghĩa, ta có \(C = \frac{{xy\left( {{x^{\frac{1}{5}}} + {y^{\frac{1}{5}}}} \right)}}{{{x^{\frac{1}{5}}} + {y^{\frac{1}{5}}}}} = xy\).
Bài 3: Rút gọn biểu thức \(E = \frac{{{a^{\sqrt 5 + 1}}.{a^{2 - \sqrt 5 }}}}{{{{({a^{\sqrt 7 - 3}})}^{\sqrt 7 + 3}}}}\) (a > 0).
Giải:
\(E = \frac{{{a^{\sqrt 5 + 1 + 2 - \sqrt 5 }}}}{{{a^{(\sqrt 7 - 3)(}}^{\sqrt 7 + 3)}}} = \frac{{{a^3}}}{{{a^{ - 2}}}} = {a^5}\).
Các bài khác cùng chuyên mục
- Bài 4.20 trang 114 SGK Toán 11 tập 1 - Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá













Danh sách bình luận