Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Bài 4. Khi nào góc xOy + góc yOz= góc xOz?
Lý thuyết Khi nào góc xOy + góc yOz = góc xOz?
1. Tính chất cộng số đo hai góc Nếu tia Oy nằm giữa hai tia Ox va Oz thì
1. Tính chất cộng số đo hai góc
Nếu tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) thì \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\).
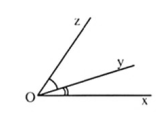
Ngược lại, nếu \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\) thì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz.\)
Lưu ý:
a) Ta có thể dùng mệnh đề tương đương sau với tính chất trên:
Nếu \(\widehat{xOy}+\widehat{yOz}\neq \widehat{xOz}\) thì tia \(Oy\) không nằm giữa hai tia \(Ox\) và \(Oz.\)
b) Cộng liên tiếp. Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ot;\) tia \(Oz\) nằm giữa hai tia \(Oy\) và \(Ot\) thì:
\(\widehat{xOy}+\widehat{yOz}+ \widehat{tO z}=\widehat{xOt}\)
2. Hai góc kề nhau, phụ nhau, bù nhau
-Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nữa mặt phẳng đối nhau bờ chứa cạnh chung.
- Hai góc phụ nhau là hai góc có tổng số đo bằng \(90^{0}\)
- Hai góc bù nhau là hai góc có tổng số đo bằng \(180^{0}\)
Lưu ý:
a) Hai góc kề bù là hai góc vừa kề nhau vừa bù nhau. Hai góc kề bù có tổng số đo bằng \(180^{0}\) .
b) Hai góc cùng phụ (hoặc cùng bù) với một góc thứ 3 thì bằng nhau.
Loigiaihay.com
Bình luận
Chia sẻ
- Trả lời câu hỏi Bài 4 trang 80 Toán 6 Tập 2
- Trả lời câu hỏi Bài 4 trang 81 Toán 6 Tập 2
- Bài 18 trang 82 SGK Toán 6 tập 2
- Bài 19 trang 82 SGK Toán 6 tập 2
- Bài 20 trang 82 SGK Toán 6 tập 2
>> Xem thêm
Tham Gia Group Dành Cho Lớp 6 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
