Lý thuyết Giải bài toán bằng cách lập phương trình bậc hai Toán 9 Cùng khám phá

Bước 1: Lập phương trình: - Chọn ẩn và đặt điều kiện cho ẩn số. - Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết. - Lập phương trình biểu thị mối quan hệ giữa các đại lượng. Bước 2. Giải phương trình. Bước 3. Kiểm tra xem nghiệm có thỏa mãn điều kiện của ẩn hay không rồi kết luận.

Bước 1: Lập phương trình:

- Chọn ẩn và đặt điều kiện cho ẩn số.

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3. Kiểm tra xem nghiệm có thỏa mãn điều kiện của ẩn hay không rồi kết luận.

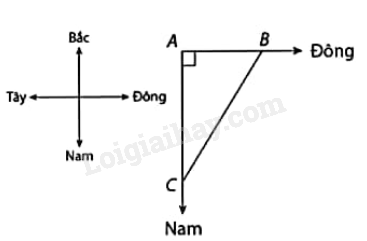
Ví dụ: Một ca nô xuất phát từ một bến và có chuyển động thẳng theo hướng Đông. Cùng lúc đó, một tàu thủy rời bến và chuyển động thẳng theo hướng Nam với tốc độ lớn hơn tốc độ của ca nô 8km/h. Tính tốc độ của ca nô, biết sau một giờ kể từ lúc xuất phát, khoảng cách giữa ca nô với tàu thủy là 40km.

Lời giải:

Gọi tốc độ của ca nô là \(x\left( {km/h} \right)\left( {x > 0} \right)\).

Tốc độ của tàu thủy là \(x + 8\left( {km/h} \right)\).

Gọi A là vị trí của bến, gọi B, C lần lượt là vị trí của ca nô và tàu thủy sau khi rời bến 1 giờ (như hình vẽ).

Quãng đường ca nô đi được sau 1 giờ là:

\(AB = x.1 = x\left( {km} \right)\)

Quãng đường tàu thủy đi được sau 1 giờ là:

\(AC = \left( {x + 8} \right).1 = x + 8\left( {km} \right)\)

Ca nô và tày thủy chuyển động theo hai hướng vuông góc với nhau nên tam giác ABC vuông tại A.

Ta có: \(A{B^2} + A{C^2} = B{C^2}\) (định lí Pythagore).

\(\begin{array}{l}{x^2} + {\left( {x + 8} \right)^2} - {40^2}\\{x^2} + {x^2} + 16x + 64 = 1600\\2{x^2} + 16x - 1536 = 0\\{x^2} + 8x - 768 = 0\end{array}\)

Ta có: \(\Delta ' = {4^2} + 768 = 784,\sqrt {\Delta '} = 28\).

Suy ra phương trình có hai nghiệm phân biệt:

\({x_1} = \frac{{ - 4 - 28}}{1} = - 32\) (loại); \({x_2} = \frac{{ - 4 + 28}}{1} = 24\) (thỏa mãn điều kiện).

Vậy tốc độ của ca nô là \(24km/h\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải câu hỏi trang 20, 21, 22 SGK Toán 9 tập 2 - Cùng khám phá
Một mảnh vườn hình chữ nhật có chiều dài gấp đôi chiều rộng. Người ta làm một lối đi quanh vườn có bề rộng 0,5 m, phần đất còn lại để trồng cây có diện 55 m2 . a) Gọi chiều rộng mảnh vườn là x (m) (x > 0). Hãy biểu diễn chiều dài mảnh vườn theo x. b) Hãy biểu diễn chiều dài và chiều rộng của phần đất trồng cây theo x. Lập phương trình biểu thị diện tích phần đất trồng cây. c) Hỏi chiều rộng và chiều dài của mảnh vườn là bao nhiêu mét? Trong Hoạt động, ta đã kí hiệu x là chiều rộng của mảnh đ
Giải bài tập 6.20 trang 22 SGK Toán 9 tập 2 - Cùng khám phá
Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 181. Tìm hai số đó.
Giải bài tập 6.21 trang 22 SGK Toán 9 tập 2 - Cùng khám phá
Một tam giác vuông có độ dài ba cạnh là các số tự nhiên liên tiếp. Tính chu vi tam giác vuông đó.
Giải bài tập 6.22 trang 22 SGK Toán 9 tập 2 - Cùng khám phá
Từ một miếng tôn hình chữ nhật, người ta cắt ở bốn góc bốn hình vuông có cạnh bằng 4 dm để tạo thành một cái thùng hình hộp chữ nhật không nắp có dung tích bằng 1536 dm3 (Hình 6.9). Tính kích thước của miếng tôn ban đầu, biết chiều dài của nó gấp đôi chiều rộng.
Giải bài tập 6.23 trang 22 SGK Toán 9 tập 2 - Cùng khám phá
Bác Trung gửi tiết kiệm 50000000 đồng vào ngân hang với kì hạn 1 năm theo hình thức lãi kép (sau 1 năm, tiền lãi sẽ được gộp vào vốn để tính lãi cho năm tiếp theo). Tổng số tiền bác Trung nhận được sau 2 năm là 56180000 đồng. Hỏi lãi suất ngân hàng bác Trung gửi là bao nhiêu phần trăm một năm, biết trong 2 năm gửi lãi suất không thay đổi và bác Trung không rút tiền ra?
Giải bài tập 6.24 trang 22 SGK Toán 9 tập 2 - Cùng khám phá
Khi nói đến ti vi loại 32 inch, ta hiểu rằng đường chéo màn hình của chiếc ti vi này dài 32 inch (1 inch \( \approx \) 2,54 cm). Khi nói đến tỉ lệ khung hình 16 : 9, ta hiểu rằng chiều dài và chiều rộng của màn hình đó lần lượt tỉ lệ với 16; 9. Loại tỉ lệ khung hình này là phổ biến nhất hiện nay. Để sản xuất một chiếc ti vi loại 32 inch với tỉ lệ khung hình 16 : 9 thì cần thiết kế chiều dài và chiều rộng màn hình bằng bao nhiêu centimét (làm tròn kết quả đến hàng phần trăm)?