Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức

1. Định nghĩa Khái niệm GTLN, GTNN của hàm số

Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa

1. Định nghĩa

Khái niệm GTLN, GTNN của hàm số

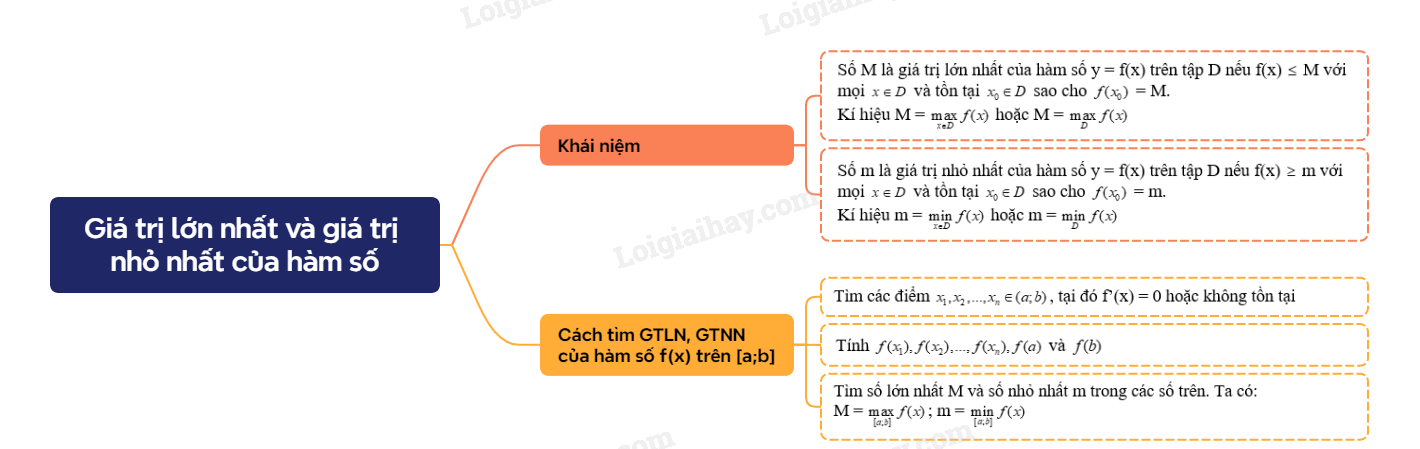
Cho hàm số y = f(x) xác định trên tập D.

- Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) $ \le $ M với mọi $x \in D$ và tồn tại ${x_0} \in D$ sao cho $f({x_0})$ = M.

Kí hiệu M = $\mathop {\max }\limits_{x \in D} f(x)$ hoặc M = $\underset{D}{\mathop{\max }}\,f(x)$

- Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) $ \ge $ m với mọi $x \in D$ và tồn tại ${x_0} \in D$ sao cho $f({x_0})$ = m.

Kí hiệu m = $\mathop {\min }\limits_{x \in D} f(x)$ hoặc m = $\mathop {\min }\limits_D f(x)$

Ví dụ: Tìm GTLN, GTNN của hàm số $y = f(x) = \sqrt {1 - {x^2}} $

Tập xác định của hàm số là $\left[ { - 1;1} \right]$

Ta có:

$f(x) = \sqrt {1 - {x^2}} $ $ \ge $ 0; dấu bằng xảy ra khi $1 - {x^2} = 0$, tức x = -1 hoặc x = 1.

Do đó $\mathop {\min }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f( - 1) = f(1) = 0$

$f(x) = \sqrt {1 - {x^2}} $ $ \le 1$; dấu bằng xảy ra khi $1 - {x^2} = 1$, tức x = 0.

Do đó $\mathop {\max }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f(0) = 1$

2. Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Giả sử y = f(x) là hàm số liên tục trên $\left[ {a;b} \right]$ và có đạo hàm trên (a;b), có thể trừ ra tại một số hữu hạn điểm mà tại đó hàm số không có đạo hàm. Giả sử chỉ có hữu hạn điểm trong đoạn $\left[ {a;b} \right]$ mà đạo hàm f’(x) = 0.

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn $\left[ {a;b} \right]$:

Tìm các điểm ${x_1},{x_2},...,{x_n} \in (a;b)$, tại đó f’(x) = 0 hoặc không tồn tại
Tính $f({x_1}),f({x_2}),...,f({x_n}),f(a)$ và $f(b)$
Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:

M = $\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)$; m = $\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)$

Ví dụ: Tìm GTLN và GTNN của hàm số $y = {x^4} - 4{x^2} + 3$ trên đoạn $\left[ {0;4} \right]$

Ta có: $y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0$ hoặc $x = \sqrt 2 $ (vì $x \in \left[ {0;4} \right]$)

y(0) = 3; y(4) = 195; y($\sqrt 2 $) = -1

Do đó: $\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195$; $\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) = - 1$

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 15,16,17 SGK Toán 12 tập 1 - Kết nối tri thức
Định nghĩa
Giải mục 2 trang 17,18,19 SGK Toán 12 tập 1 - Kết nối tri thức
Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
Giải bài tập 1.10 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = - {x^2} + 4x + 3); b) (y = {x^3} - 2{x^2} + 1) trên (left[ {0; + infty } right)); c) (y = frac{{{x^2} - 2x + 3}}{{x - 1}}) trên (left( {1; + infty } right)); d) (y = sqrt {4x - 2{x^2}} ).
Giải bài tập 1.11 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = {x^4} - 2{x^2} + 3); b) (y = x.{e^{ - x}}); c) (y = xln x); d) (y = sqrt {x - 1} + sqrt {3 - x} ).
Giải bài tập 1.12 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = 2{x^3} - 6x + 3) trên đoạn (left[ { - 1;2} right]); b) (y = {x^4} - 3{x^2} + 2) trên đoạn (left[ {0;3} right]); c) (y = x - sin 2x) trên đoạn (left[ {0;pi } right]); d) (y = left( {{x^2} - x} right){e^x}) trên đoạn (left[ {0;1} right]).
Giải bài tập 1.13 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Giải bài tập 1.14 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng (108c{m^2}) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Giải bài tập 1.15 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích $1\;000c{m^3}$. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/$c{m^2}$, trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/$c{m^2}$. Tìm các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.