Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số ..

Giải mục 1 trang 15,16,17 SGK Toán 12 tập 1 - Kết nối tri thức

Định nghĩa

Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1
LT1

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 15 SGK Toán 12 Kết nối tri thức

Cho hàm số \(y = f\left( x \right) = {x^2} - 2x\) với \(x \in \left[ {0;3} \right]\), có đồ thị như Hình 1.15.

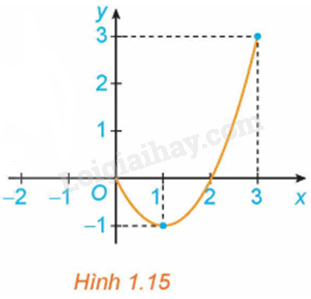
a) Giá trị lớn nhất M của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = M\).

b) Giá trị nhỏ nhất m của hàm số trên đoạn \(\left[ {0;3} \right]\) là bao nhiêu? Tìm \({x_0}\) sao cho \(f\left( {{x_0}} \right) = m\).

Phương pháp giải:

Sử dụng kiến thức về đọc hiểu đồ thị hàm số.

Lời giải chi tiết:

a) Giá trị lớn nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(M = 3\).

Với \({x_0} = 3\) thì \(f\left( 3 \right) = 3\).

b) Giá trị nhỏ nhất của đồ thị hàm số trên đoạn \(\left[ {0;3} \right]\) là \(m = - 1\).

Với \({x_0} = 1\) thì \(f\left( 1 \right) = - 1\).

LT1

Trả lời câu hỏi Luyện tập 1 trang 17 SGK Toán 12 Kết nối tri thức

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) \(y = \sqrt {2x - {x^2}} \);

b) \(y = - x + \frac{1}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\).

Phương pháp giải:

Sử dụng kiến thức về khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số để tính: Cho hàm số \(y = f\left( x \right)\) xác định trên tập D.

+ Số M được gọi là giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \le M\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = M\).

Kí hiệu \(M = \mathop {\max }\limits_{x \in D} f\left( x \right)\) hoặc \(M = \mathop {\max }\limits_D f\left( x \right)\)

+ Số m được gọi là giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên tập D nếu \(f\left( x \right) \ge m\) với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f\left( {{x_0}} \right) = m\).

Kí hiệu \(m = \mathop {\min }\limits_{x \in D} f\left( x \right)\) hoặc \(m = \mathop {\min }\limits_D f\left( x \right)\)

Lời giải chi tiết:

a) Tập xác định của hàm số là \(\left[ {0;2} \right]\).

Với \(x \in \left[ {0;2} \right]\) ta có: \(y' = \frac{{\left( {2x - {x^2}} \right)'}}{{2\sqrt {2x - {x^2}} }} = \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }}\), \(y' = 0 \Leftrightarrow \frac{{ - x + 1}}{{\sqrt {2x - {x^2}} }} = 0 \Leftrightarrow x = 1\left( {tm} \right)\)

Lập bảng biến thiên của hàm số trên đoạn \(\left[ {0;2} \right]\):

Từ bảng biến thiên ta thấy: \(\mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 0 \right) = f\left( 2 \right) = 0,\mathop {\max }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = f\left( 1 \right) = 1\).

b) Với \(x \in \left( {1; + \infty } \right)\) ta có:

Ta có: \(y' = - 1 + \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}} < 0\;\forall x \in \left( {1; + \infty } \right)\)

\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( { - x + \frac{1}{{x - 1}}} \right) = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \left( { - x + \frac{1}{{x - 1}}} \right) = - \infty \)

Lập bảng biến thiên của hàm số trên \(\left( {1; + \infty } \right)\):

Vậy hàm số không có giá trị lớn nhất, giá trị nhỏ nhất trên \(\left( {1; + \infty } \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.2 trên 5 phiếu

Bài tiếp theo

Giải mục 2 trang 17,18,19 SGK Toán 12 tập 1 - Kết nối tri thức
Cách tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
Giải bài tập 1.10 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = - {x^2} + 4x + 3); b) (y = {x^3} - 2{x^2} + 1) trên (left[ {0; + infty } right)); c) (y = frac{{{x^2} - 2x + 3}}{{x - 1}}) trên (left( {1; + infty } right)); d) (y = sqrt {4x - 2{x^2}} ).
Giải bài tập 1.11 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = {x^4} - 2{x^2} + 3); b) (y = x.{e^{ - x}}); c) (y = xln x); d) (y = sqrt {x - 1} + sqrt {3 - x} ).
Giải bài tập 1.12 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau: a) (y = 2{x^3} - 6x + 3) trên đoạn (left[ { - 1;2} right]); b) (y = {x^4} - 3{x^2} + 2) trên đoạn (left[ {0;3} right]); c) (y = x - sin 2x) trên đoạn (left[ {0;pi } right]); d) (y = left( {{x^2} - x} right){e^x}) trên đoạn (left[ {0;1} right]).
Giải bài tập 1.13 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Giải bài tập 1.14 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng (108c{m^2}) như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
Giải bài tập 1.15 trang 19 SGK Toán 12 tập 1 - Kết nối tri thức
Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích \(1\;000c{m^3}\). Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/\(c{m^2}\), trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/\(c{m^2}\). Tìm các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức
1. Định nghĩa Khái niệm GTLN, GTNN của hàm số