Lý thuyết Định lí Pythagore SGK Toán 8 - Cánh diều

Định lí Pythagore

1. Định lí Pythagore

Trong một tam giác vuông, bình phương độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.

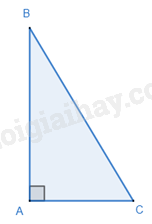
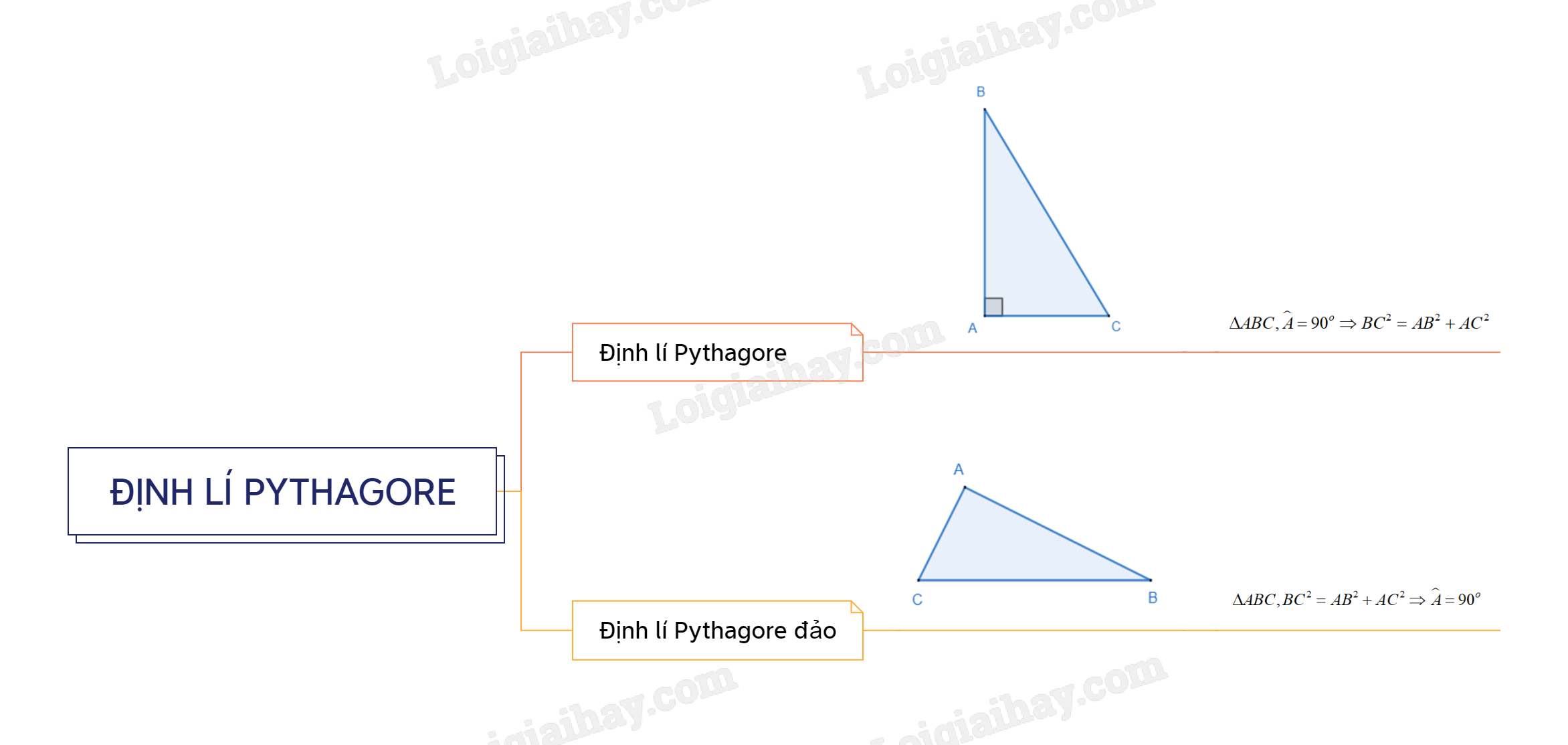
\(\Delta ABC,\widehat A = {90^o} \) suy ra \(B{C^2} = A{B^2} + A{C^2}\)

2. Định lí Pythagore đảo

Nếu một tam giác có bình phương độ dài của một cạnh bằng tổng các bình phương độ dài của hai cạnh kia thì tam giác đó là tam giác vuông.

\(\Delta ABC,B{C^2} = A{B^2} + A{C^2} \) suy ra \( \widehat A = {90^o}\)

Ví dụ:

Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do \({3^2} + {4^2} = {5^2}\), suy ra \(B{C^2} = A{B^2} + A{C^2}\).

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 9 phiếu

Giải Câu hỏi mở đầu trang 94 SGK Toán 8 – Cánh diều
Quan sát Hình 1,
Giải mục 1 trang 94, 95 SGK Toán 8 tập 1 - Cánh diều
Thực hiện các hoạt động sau: a) Vẽ và cắt giấy để có 4 hình tam giác vuông như nhau với độ dài cạnh huyền là a, độ dài hai cạnh góc vuông là b và c, trong đó a, b, c có cùng đơn vị độ dài (Hình 2)
Giải mục 2 trang 95, 96 SGK Toán 8 tập 1 - Cánh diều
Thực hiện các hoạt động sau: a) Vẽ một tam giác ABC có AB = 3 cm, AC = 4 cm và BC = 5 cm b) Tính và so sánh diện tích của hình vuông có cạnh BC với tổng diện tích của hai hình vuông tương ứng có cạnh AB và AC. c) Kiểm tra xem các góc A của tam giác ABc có phải là góc vuông hay không?
Giải bài 1 trang 96 SGK Toán 8 tập 1 - Cánh diều
Cho tam giác ABC vuông tại A.
Giải bài 2 trang 96 SGK Toán 8 tập 1 - Cánh diều
Tam giác có độ dài ba cạnh
Giải bài 3 trang 97 SGK Toán 8 tập 1 - Cánh diều
Cho tam giác vuông cân
Giải bài 4 trang 97 SGK Toán 8 tập 1 - Cánh diều
Cho một tam giác đều cạnh a
Giải bài 5 trang 97 SGK Toán 8 tập 1 - Cánh diều
Hình 9 mô tả một thanh gỗ dài
Giải bài 6 trang 97 SGK Toán 8 tập 1 - Cánh diều
Hình 10 mô tả mặt cắt đứng