Lý thuyết Đa giác đều Toán 9 Cùng khám phá

1. Đa giác Đa giác ABCDE: + Các đỉnh là các điểm: A, B, C, D, E; + Các cạnh là các đoạn thẳng: AB, BC, CD, DE, AE; + Các cặp đỉnh kề nhau là: A và B, B và C, C và D, D và E, E và A;

1. Đa giác

Đa giác ABCDE:

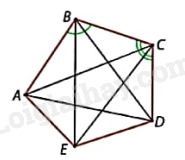
+ Các đỉnh là các điểm: A, B, C, D, E;

+ Các cạnh là các đoạn thẳng: AB, BC, CD, DE, AE;

+ Các cặp đỉnh kề nhau là: A và B, B và C, C và D, D và E, E và A;

+ Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, AD, BD, BE, CE;

+ Các góc \(\widehat {ABC},\widehat {BCD},\widehat {CDE},\widehat {DEA},\widehat {EAB}\).

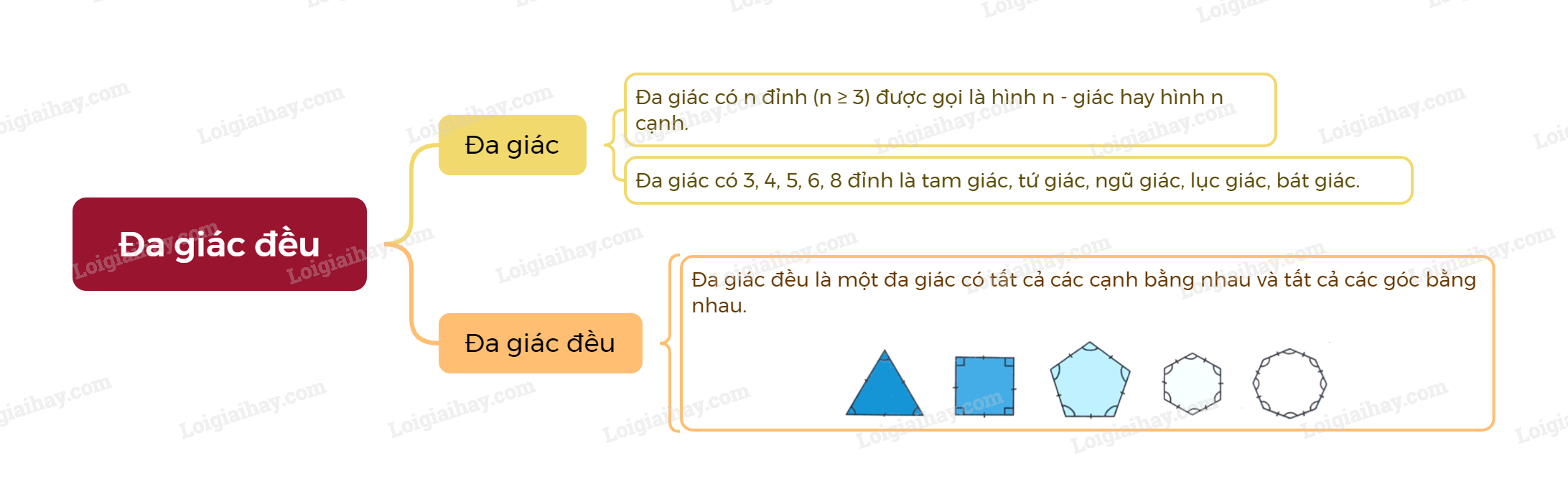
- Đa giác có n đỉnh (\(n \ge 3\)) được gọi là hình n – giác hay hình n cạnh,

Ta thường gọi các đa giác có 3, 4, 5, 6, 8 đỉnh là tam giác, tứ giác, ngũ giác, lục giác, bát giác.

2. Đa giác đều

Đa giác đều là một đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Ví dụ: Một số hình đa giác đều thường gặp trong hình học:

3. Một số hình phẳng đều trong thực tiễn

Ví dụ: Một số hình phẳng đều trong thực tế:

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 42, 43 SGK Toán 9 tập 2 - Cùng khám phá
Trong Hình 8.1, hãy cho biết những hình nào có tính chất: Tạo bởi các đoạn thẳng AB, BC, CD, DE, EA; Bất kì hai đoạn thẳng nào có một điểm chung cũng không cùng nằm trên một đường thẳng.
Giải mục 2 trang 44, 45 SGK Toán 9 tập 2 - Cùng khám phá
Cho các đa giác trong Bảng 8.1. So sánh các cạnh và các góc của mỗi đa giác, cho biết các đa giác ở cột B có đặc điểm gì khác so với đa giác tương ứng ở cột A.
Giải mục 3 trang 47 SGK Toán 9 tập 2 - Cùng khám phá
Kể tên các loại đa giác đều trong hoạ tiết ở Hình 8.13.
Giải bài tập 8.1 trang 48 SGK Toán 9 tập 2 - Cùng khám phá
Kể tên các loại đa giác đều có trong Hình 8.14.
Giải bài tập 8.2 trang 48 SGK Toán 9 tập 2 - Cùng khám phá
Tìm các số thích hợp cho các ô ? trong Bảng 8.2:
Giải bài tập 8.3 trang 48 SGK Toán 9 tập 2 - Cùng khám phá
Cho ngũ giác đều MNPQR như Hình 8.15. Kể tên các đỉnh, các góc, các cạnh và đường chéo của ngũ giác đều.
Giải bài tập 8.4 trang 48 SGK Toán 9 tập 2 - Cùng khám phá
Cho ngũ giác đều ABCDE như Hình 8.16. a) Tính tổng các góc trong tam giác ABC, ACD, ADE, từ đó suy ra tổng các góc trong ngũ giác đều ABCDE. b) Tính số đo góc E.
Giải bài tập 8.5 trang 48 SGK Toán 9 tập 2 - Cùng khám phá
Kể tên các loại các loại đa giác đều trong mỗi trường hợp ở Hình 8.17.