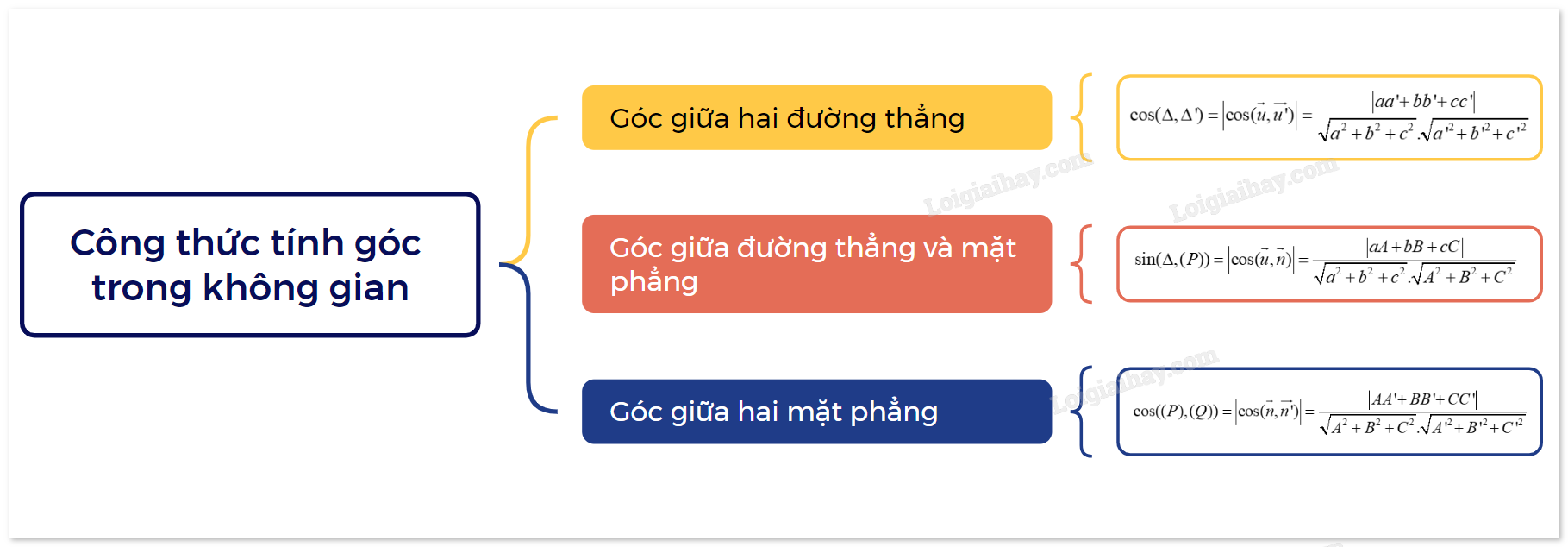
Lý thuyết Công thức tính góc trong không gian Toán 12 Kết nối tri thức

1. Công thức tính góc giữa hai đường thẳng

1. Công thức tính góc giữa hai đường thẳng

Trong không gian Oxyz, cho hai đường thẳng \(\Delta \) và \(\Delta '\) tương ứng có vecto chỉ phương \(\overrightarrow u = (a;b;c),\overrightarrow {u'} = (a';b';c')\). Khi đó:

\(\cos (\Delta ,\Delta ') = \left| {\cos (\overrightarrow u ,\overrightarrow {u'} )} \right| = \frac{{\left| {aa' + bb' + cc'} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {a{'^2} + b{'^2} + c{'^2}} }}\)

2. Công thức tính góc giữa đường thẳng và mặt phẳng

Trong không gian Oxyz, cho đường thẳng \(\Delta \) có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) và mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n = (A;B;C)\). Khi đó:

\(\sin (\Delta ,(P)) = \left| {\cos (\overrightarrow u ,\overrightarrow n )} \right| = \frac{{\left| {aA + bB + cC} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{A^2} + {B^2} + {C^2}} }}\)

3. Công thức tính góc giữa hai mặt phẳng

Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vecto pháp tuyến \(\overrightarrow n = (A;B;C),\overrightarrow {n'} = (A';B';C')\). Khi đó, góc giữa (P) và (Q), kí hiệu là ((P), (Q)), được tính theo công thức:

\(\cos ((P),(Q)) = \left| {\cos (\overrightarrow n ,\overrightarrow {n'} )} \right| = \frac{{\left| {AA' + BB' + CC'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} .\sqrt {A{'^2} + B{'^2} + C{'^2}} }}\)

Bình luận

Chia sẻ

Bình chọn:

4 trên 5 phiếu

Bài tiếp theo

Giải câu hỏi mở đầu trang 50 SGK Toán 12 tập 2 - Kết nối tri thức
Một mái nhà hình tròn được đặt trên ba cây cột trụ (H.5.33). Các cây cột vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 7 m, 6 m, 5 m.
Giải mục 1 trang 50,51 SGK Toán 12 tập 2 - Kết nối tri thức
CÔNG THỨC TÍNH GÓC GIỮA HAI ĐƯỜNG THẲNG
Giải mục 2 trang 51 SGK Toán 12 tập 2 - Kết nối tri thức
CÔNG THỨC TÍNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Giải mục 3 trang 52,53 SGK Toán 12 tập 2 - Kết nối tri thức
CÔNG THỨC TÍNH GÓC GIỮA HAI MẶT PHẲNG
Giải bài tập 5.20 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Trong không gian Oxyz, tính góc giữa hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - t\\z = 2 + 3t\end{array} \right.\) và \({\Delta _2}:\frac{{x - 2}}{{ - 1}} = \frac{{x + 1}}{1} = \frac{{z - 2}}{2}\).
Giải bài tập 5.21 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Trong không gian Oxyz, tính góc giữa trục Oz và mặt phẳng \(\left( P \right):x + 2y - z - 1 = 0\).
Giải bài tập 5.22 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Tính góc giữa đường thẳng \(\Delta :\frac{{x + 1}}{{ - 1}} = \frac{{y - 3}}{2} = \frac{{z + 2}}{3}\) và mặt phẳng \(\left( P \right):x + y + z + 3 = 0\).
Giải bài tập 5.23 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Kim tự tháp Kheops ở Ai Cập có dạng hình chóp S. ABCD, có đáy là hình vuông với cạnh dài 230m, các cạnh bên bằng nhau và dài 219m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng (SAB) và (SBC).
Giải bài tập 5.24 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
(H.5.39) Trong một bể hình lập phương cạnh 1m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40cm, 44cm, 48cm. a) Khoảng cách từ điểm D đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên.) b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?