Giải câu hỏi mở đầu trang 50 SGK Toán 12 tập 2 - Kết nối tri thức

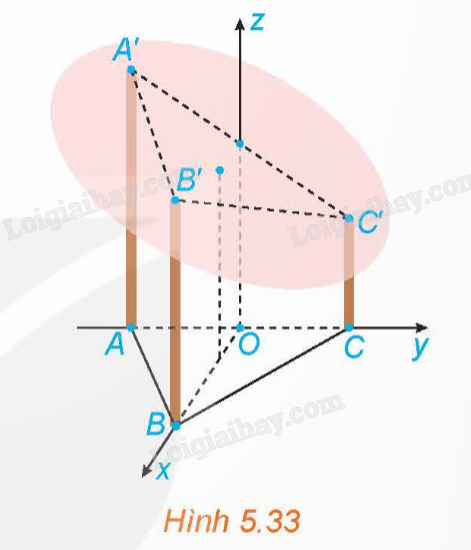
Một mái nhà hình tròn được đặt trên ba cây cột trụ (H.5.33). Các cây cột vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 7 m, 6 m, 5 m.

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Một mái nhà hình tròn được đặt trên ba cây cột trụ (H.5.33). Các cây cột vuông góc với mặt sàn nhà phẳng và có độ cao lần lượt là 7 m, 6 m, 5 m. Ba chân cột là ba đỉnh của một tam giác đều trên mặt sàn nhà với cạnh dài 4 m. Hỏi mái nhà nghiêng với mặt sàn nhà một góc bao nhiêu độ?

Phương pháp giải - Xem chi tiết

Tìm vecto pháp tuyến của hai mặt phẳng (ABC), (A’B’C’) rồi áp dụng công thức tính góc giữa hai mặt phẳng.

Quảng cáo

Lời giải chi tiết

Hệ trục tọa độ được gắn như hình vẽ.

Gọi góc giữa mái nhà và mặt sàn là \(\alpha \). Ta có \(\alpha = \left( {(ABC),(A'B'C')} \right)\).

Vì ABC là tam giác đều, mà BO là đường cao (trục Ox vuông góc với Oy) nên BO đồng thời là đường trung tuyến. Do đó, O là trung điểm của AC, suy ra \(AO = OC = \frac{{AC}}{2} = 2\) (m).

Vì BO là đường trung truyến của tam giác đều có cạnh bằng 4 m nên \(BO = \frac{{4\sqrt 3 }}{2} = 2\sqrt 3 \).

Khi đó, ta có tọa độ các điểm: \(A'\left( {0; - 2;7} \right)\), \(B'\left( {2\sqrt 3 ;0;6} \right)\), \(C'\left( {0;2;5} \right)\).

Suy ra \(\overrightarrow {A'B'} = \left( {2\sqrt 3 ;2; - 1} \right)\), \(\overrightarrow {A'C'} = \left( {0;4; - 2} \right)\).

Ta có \(\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}2&{ - 1}\\4&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{ - 1}&{2\sqrt 3 }\\{ - 2}&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}{2\sqrt 3 }&2\\0&4\end{array}} \right|} \right) = \left( {0;4\sqrt 3 ;8\sqrt 3 } \right)\).

Suy ra \(\overrightarrow n = \frac{1}{{4\sqrt 3 }}\left[ {\overrightarrow {A'B'} ,\overrightarrow {A'C'} } \right] = \left( {0;1;2} \right)\) là một vecto pháp tuyến của (A’B’C’).

Sàn nhà trùng với mặt phẳng tọa độ (Oxy) nên có vecto pháp tuyến là \(\overrightarrow k = \left( {0;0;1} \right)\).

Ta có \(\cos \alpha = \frac{{\left| {0.0 + 0.1 + 1.2} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {1^2} + {2^2}} }} = \frac{2}{{\sqrt 5 }} \Rightarrow \alpha \approx 26,{6^o}\).

Vậy mái nhà nghiêng với mặt sàn nhà một góc khoảng \(26,{6^o}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 50,51 SGK Toán 12 tập 2 - Kết nối tri thức
CÔNG THỨC TÍNH GÓC GIỮA HAI ĐƯỜNG THẲNG
Giải mục 2 trang 51 SGK Toán 12 tập 2 - Kết nối tri thức
CÔNG THỨC TÍNH GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Giải mục 3 trang 52,53 SGK Toán 12 tập 2 - Kết nối tri thức
CÔNG THỨC TÍNH GÓC GIỮA HAI MẶT PHẲNG
Giải bài tập 5.20 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Trong không gian Oxyz, tính góc giữa hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 - t\\z = 2 + 3t\end{array} \right.\) và \({\Delta _2}:\frac{{x - 2}}{{ - 1}} = \frac{{x + 1}}{1} = \frac{{z - 2}}{2}\).
Giải bài tập 5.21 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Trong không gian Oxyz, tính góc giữa trục Oz và mặt phẳng \(\left( P \right):x + 2y - z - 1 = 0\).
Giải bài tập 5.22 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Tính góc giữa đường thẳng \(\Delta :\frac{{x + 1}}{{ - 1}} = \frac{{y - 3}}{2} = \frac{{z + 2}}{3}\) và mặt phẳng \(\left( P \right):x + y + z + 3 = 0\).
Giải bài tập 5.23 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
Kim tự tháp Kheops ở Ai Cập có dạng hình chóp S. ABCD, có đáy là hình vuông với cạnh dài 230m, các cạnh bên bằng nhau và dài 219m (theo britannica.com) (H.5.38). Tính góc giữa hai mặt phẳng (SAB) và (SBC).
Giải bài tập 5.24 trang 53 SGK Toán 12 tập 2 - Kết nối tri thức
(H.5.39) Trong một bể hình lập phương cạnh 1m có chứa một ít nước. Người ta đặt đáy bể nghiêng so với mặt phẳng nằm ngang. Biết rằng, lúc đó mặt nước có dạng hình bình hành ABCD và khoảng cách từ các điểm A, B, C đến đáy bể tương ứng là 40cm, 44cm, 48cm. a) Khoảng cách từ điểm D đến đáy bể bằng bao nhiêu centimét? (Tính gần đúng, lấy giá trị nguyên.) b) Đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiêu độ?
Lý thuyết Công thức tính góc trong không gian Toán 12 Kết nối tri thức
1. Công thức tính góc giữa hai đường thẳng