-
Toán 8 tập 1 - Chân trời sáng tạo
-
Toán 8 tập 2 - Chân trời sáng tạo
Toán 8, giải toán lớp 8 chân trời sáng tạo
Bài 2. Các trường hợp đồng dạng của hai tam giác Toán 8..
Giải mục 3 trang 69, 70 SGK Toán 8 tập 2– Chân trời sáng tạo
Cho hai tam giác
HĐ3
Video hướng dẫn giải
Cho hai tam giác ABC và A′B′C′ có ˆA=^A′,ˆC=^C′ (Hình 9).
Trên cạnh AC, lấy điểm D sao cho DC=A′C′. Qua D là kẻ đường thẳng song song với AB cắt cạnh BC tại E.
a) Tam giác DEC có đồng dạng với tam giác ABC không?
b) Nhận xét về mối quan hệ giữa tam giác A′B′C′và tam giác DEC.
c) Dự đoán về sự đồng dạng của hai tam giác A′B′C′và ABC.
Phương pháp giải:
- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
- Hai tam giác bằng nhau thì đồng dạng với nhau.
Lời giải chi tiết:
a) Vì ED//AB⇒ΔDEC∽ΔABC (định lí)
b) Vì ED//AB⇒^CDE=^CAB (hai góc đồng vị)
Mà ^CAB=^A′. Do đó, ^CDE=^B′A′C′.
Xét tam giác A′B′C′ và tam giác DEC ta có:
^B′A′C′=^CDE (chứng minh trên)
A′C′=CD (giải thuyết)
^C′=ˆC (giả thuyết)
Do đó, ΔA′B′C′=ΔDEC (g.c.g)
c) Vì tam giác ΔA′B′C′∽ΔDEC (tính chất)
Mà ΔDEC∽ΔABC nên ΔABC∽ΔA′B′C′.
TH3
Video hướng dẫn giải
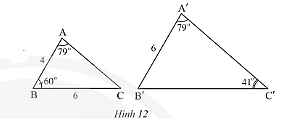
Quan sát Hình 12.
a) Chứng minh ΔABC∽ΔA′B′C′.
b) Tính độ dài cạnh B′C′.
Phương pháp giải:
- Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
- Tổng ba góc trong một tam giác có số đo bằng 180∘.
Lời giải chi tiết:
a) Xét tam giác A′B′C′ ta có:
^A′+^B′+^C′=180∘
Thay số: 79∘+^B′+41∘=180∘
⇒^B′=180∘−79∘−41∘=60∘
Xét ΔABC và ΔA′B′C′ ta có:
ˆA=^A′=79∘ (giả thuyết)
ˆB=^B′=60∘ (chứng minh trên)
Do đó, ΔABC∽ΔA′B′C′ (g.g)
b) Vì ΔABC∽ΔA′B′C′ nên ABA′B′=BCB′C′ (các cạnh tương ứng có cùng tỉ lệ)
Thay số, 46=6B′C′⇒B′C′=6.64=9
Vậy B′C′=9.
VD1
Video hướng dẫn giải
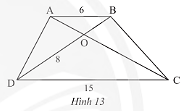
Cho hình thang ABCD(AB//CD) có AB=6m,CD=15m,OD=8m (Hình 13). Tính độ dài đoạn thẳng OB.
Phương pháp giải:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Vì tứ giác ABCD là hình thang có AB//CD nên ^BAO=^OCD (hai góc so le trong)
Xét tam giác ABO và tam giác CDO có:
^BAO=^OCD (chứng minh trên)
^AOB=^COD (hai góc đối đỉnh)
Do đó, ΔABO∽ΔCDO (g.g)
Ta có: ABCD=OBOD (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, 615=OB8⇒OB=6.815=3,2
Vậy OB=3,2m.
VD2
Video hướng dẫn giải
Qua các trường hợp đồng dạng của hai tam giác, hãy trả lời câu hỏi ở đầu bài (trang 67).
Phương pháp giải:
Dựa vào cách chứng minh hai tam giác bằng nhau và hai tam giác đồng dạng.
Lời giải chi tiết:
- Ở hai tam giác bằng nhau yêu cầu các cạnh tương ứng bằng nhau còn ở hai tam giác đồng dạng yêu cầu các cạnh tương ứng có cùng tỉ lê.
- Hai tam giác bằng nhau có ba trường hợp: cạnh góc cạnh, cạnh cạnh cạnh, góc cạnh góc.
- Hai tam giác đồng dạng có ba trường hợp: cạnh góc cạnh, cạnh cạnh cạnh, góc góc.
Bình luận
Chia sẻ
- Giải bài 1 trang 70 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 2 trang 70 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 3 trang 70 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 4 trang 71 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 5 trang 71 SGK Toán 8 tập 2– Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
