Giải mục 3 trang 42, 43, 44, 45 SGK Toán 11 tập 2 - Cùng khám phá

Hoạt động 6

Xét hàm số \(y = \sin x\)

Cho biết \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\). Bằng định nghĩa hãy tính đạo hàm của hàm số \(y = \sin x\) tại điểm \({x_0}\) bất kì.

Phương pháp giải:

Sử dụng định nghĩa để tính đạo hàm của hàm số

Lời giải chi tiết:

Với mọi \({x_0} \in R\) ta có:

\(\mathop {\lim }\limits_{x \to {x_0}} \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}} - {\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{x}}_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{2.\cos \frac{{x + {x_0}}}{2}.\sin \frac{{x - {x_0}}}{2}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \cos \frac{{x + {x_0}}}{2}.\mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin \frac{{x - {x_0}}}{2}}}{{\frac{{x - {x_0}}}{2}}} = \cos {x_0}\)

Vậy \({y'} = \cos x\)

Quảng cáo

Hoạt động 7

a, Từ công thức \(\cos x = \sin (\frac{\pi }{2} - x)\) và quy tắc tính đạo hàm của hàm hợp, chứng minh rằng: \({(\cos x)'} =  - \sin x\)

b, Từ các công thức \(\tan x = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}{{\cos x}}\), \(\cot x = \frac{{\cos x}}{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}\) và các quy tắc tính đạo hàm của thương, chứng minh rằng: \({(\tan x)'} = \frac{1}{{{{\cos }^2}x}}\) và \({(\cot x)'} = \frac{{ - 1}}{{{{\sin }^2}x}}\)

Phương pháp giải:

a, Sử dụng hàm hợp và \({({\mathop{\rm s}\nolimits} {\rm{inx}})'} = \cos x\)

b, Sử dụng quy tắc \({(\frac{u}{v})'} = \frac{{{u'}.v - u.{v'}}}{{{v^2}}}\)

Lời giải chi tiết:

a, Ta có: \({(\cos x)'} = {{\rm{[}}\sin (\frac{\pi }{2} - x){\rm{]}}'} = \cos (\frac{\pi }{2} - x).{(\frac{\pi }{2} - x)'} =  - \cos (\frac{\pi }{2} - x) =  - {\mathop{\rm s}\nolimits} {\rm{inx}}\)

b, Ta có: \({(\tan x)'} = \frac{{{{({\mathop{\rm s}\nolimits} {\rm{inx)}}}'}.\cos x - {\mathop{\rm s}\nolimits} {\rm{inx}}.{{(\cos x)}'}}}{{{{\cos }^2}x}} = \frac{{{{\cos }^2}x + {{\sin }^2}x}}{{{{\cos }^2}x}} = \frac{1}{{{{\cos }^2}x}}\)

               \({(\cot x)'} = \frac{{{{(\cos x)}'}.{\mathop{\rm s}\nolimits} {\rm{inx}} - \cos x.{{({\mathop{\rm s}\nolimits} {\rm{inx}})}'}}}{{{\mathop{\rm s}\nolimits} {\rm{i}}{{\rm{n}}^2}{\rm{x}}}} = \frac{{ - ({{\sin }^2}x + {{\cos }^2}x)}}{{{{\sin }^2}x}} = \frac{{ - 1}}{{{{\sin }^2}x}}\)

Luyện tập 6

Tính đạo hàm các hàm số sau:

a, \(y = 3\cot x - \frac{{\tan x}}{2} + 1\)                              

b, \(y = \frac{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}{x}\)

Phương pháp giải:

Sử dụng các quy tắc :\({(\tan x)'} = \frac{1}{{{{\cos }^2}x}}\) ,\({(\cot x)'} = \frac{{ - 1}}{{{{\sin }^2}x}}\), \({({\mathop{\rm s}\nolimits} {\rm{inx}})'} = \cos x\)

Lời giải chi tiết:

a, \({y'} = {(3\cot x - \frac{{\tan x}}{2} + 1)'} = \frac{{ - 3}}{{{{\sin }^2}x}} - \frac{1}{{2{{\cos }^2}x}}\)

b, \({y'} = {(\frac{{{\mathop{\rm s}\nolimits} {\rm{inx}}}}{x})'} = \frac{{{{({\mathop{\rm s}\nolimits} {\rm{inx}})}'}.x - {x'}.{\mathop{\rm s}\nolimits} {\rm{inx}}}}{{{x^2}}} = \frac{{\cos x.x - {\mathop{\rm s}\nolimits} {\rm{inx}}}}{{{x^2}}}\)

Vận dụng 2

Phương trình chuyển động của một con lắc lò xo quanh vị trí cân bằng O là \(x = 4.\cos 2t\), trong đó t được tính bằng giây và x được tính bằng cm. Biết rằng vận tốc của con lắc ở thời điểm t được tính bởi \(v(t) = {x'}(t)\)

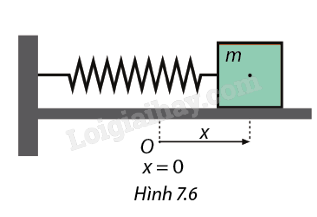
a, Tính vận tốc của con lắc tại thời điểm \(t = \frac{{7\pi }}{{12}}\)

b, Tìm thời điểm đầu tiên con lắc đạt vận tốc lớn nhất

Phương pháp giải:

a, Tính  \(v(t) = {x'}(t)\) và thay \(t = \frac{{7\pi }}{{12}}\)

b, Từ câu a tìm thời điểm con lắc đạt vận tốc lớn nhất

Lời giải chi tiết:

a, Ta có: \(v(t) = {x'}(t) = {(4.\cos 2t)'} = 4.2. - \sin 2t =  - 8.\sin 2t\)

Thay \(t = \frac{{7\pi }}{{12}}\) ta được: \(v(\frac{{7\pi }}{{12}}) =  - 8\sin \left( {2.\frac{{7\pi }}{{12}}} \right) =  - 8.\sin \left( {\frac{{7\pi }}{6}} \right) = 4\) (cm/s)

b, Ta có: \( - 1 \le \sin 2t \le 1\)\( \Rightarrow  - 8 \le  - 8\sin 2t \le 8\)

Con lắc đạt vận tốc lớn nhất khi sin 2t=-1\( \Rightarrow 2t = \frac{{3\pi }}{2} \Rightarrow t = \frac{{3\pi }}{4}\)

Hoạt động 8

Xét hàm số \(y = {e^x}\)

Cho biết \(\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x} = 1.\)Bằng định nghĩa tính đạo hàm của hàm số \(y = {e^x}\) tại điểm \({x_0}\) bất kì.

Phương pháp giải:

Sử dụng định nghĩa để tính đạo hàm

Lời giải chi tiết:

Với mọi \({x_0} \in R\) ta có:

\(\mathop {\lim }\limits_{x \to {x_0}} \frac{{{e^x} - {e^{{x_0}}}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{({e^{x - {x_0}}} - 1){e^{{x_0}}}}}{{x - {x_0}}} = {e^{{x_0}}}\)

Vậy \({y'} = {e^x}\).

Hoạt động 9

a, Từ công thức \({a^x} = {e^{x\ln a}}\) và quy tắc tính đạo hàm của hàm hợp, hãy tìm công thức tính đạo hàm của hàm số \(y = {a^x}\)

b, Từ công thức \({\log _a}x = \frac{{\ln x}}{{\ln a}}\) và các quy tắc tính đạo hàm đã biết, hãy tìm công thức tính đạo hàm của hàm số \(y = {\log _a}x\)

Phương pháp giải:

a, Sử dụng công thức \({({e^x})'} = {e^x}\)

b, Sử dụng quy tắc \({(\frac{u}{v})'} = \frac{{{u'}.v - u.{v'}}}{{{v^2}}}\)

Lời giải chi tiết:

a, Ta có: \({({a^x})'} = {({e^{x\ln a}})'} = {(x.\ln a)'}.{e^{x.\ln a}} = \ln a.{e^{x.\ln a}} = \ln a.{a^x}\)

b, Ta có: \({({\log _a}x)'} = {(\frac{{\ln x}}{{\ln a}})'} = \frac{{{{(\ln x)}'}.\ln a - \ln x.{{(\ln a)}'}}}{{{{\ln }^2}a}} = \frac{{\frac{1}{x}.\ln a}}{{{{\ln }^2}a}} = \frac{1}{{x.\ln a}}\)

Luyện tập 7

Tính đạo hàm các hàm số sau:

a,\(y = {4^{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}\)                   

b, \(y = \ln (1 + \sqrt x )\)                         

c, \(y = \frac{{\ln x}}{x}\)

Phương pháp giải:

a, Sử dụng đạo hàm hàm hợp \({y'} = {({a^u})'} = {u'}{a^u}.\ln a\)

b, Sử dụng đạo hàm hàm hợp \({y'} = {(\ln u)'} = \frac{{{u'}}}{u}\)

c, Sử dụng quy tắc \({(\frac{u}{v})'} = \frac{{{u'}.v - u.{v'}}}{{{v^2}}}\)

Lời giải chi tiết:

a, Ta có: \(\begin{array}{l}{y'} = {({4^{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}})'} = {({\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x)'}{.4^{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}.\ln 4\\ = (\cos x - \sin x){.4^{{\mathop{\rm s}\nolimits} {\rm{inx}} + \cos x}}.\ln 4\end{array}\)

b, Ta có: \({y'} = {{\rm{[}}\ln (1 + \sqrt x ){\rm{]}}'} = \frac{{{{(1 + \sqrt x )}'}}}{{1 + \sqrt x }} = \frac{1}{{2\sqrt x .(1 + \sqrt x )}}\)

c, Ta có: \({y'} = {(\frac{{\ln x}}{x})'} = \frac{{{{(\ln x)}'}.x - {x'}.\ln x}}{{{x^2}}} = \frac{{1 - \ln x}}{{{x^2}}}\)

Vận dụng 3

Nồng độ C (\(\eta g/l\)) của loại thuốc A một người uống vào sau t giờ cho bởi hàm số sau \(C(t) = 6,2.{t^4}.{e^{ - 0,5t}}\). Biết rằng nồng độ C sẽ tăng lên trong 8 giờ đầu tiên và tốc độ tăng của nồng độ C tại thời điểm t được tính bởi công thức \({C'}(t)\):

a, Tính tốc độ tăng nồng độ của thuốc A tại thời điểm \({t_0} = 1\)

b, Trong hai thời điểm \({t_0} = 1\) và \({t_1} = 5\) thời điểm nào nồng độ thuốc A tăng nhanh hơn?

Phương pháp giải:

a, Tính đạo hàm của hàm số C(t) và thay \({t_0} = 1\)

b, Thay \({t_0} = 1\) và \({t_1} = 5\) và so sánh

Lời giải chi tiết:

a, Ta có:

\(\begin{array}{l}{C'}(t) = {(6,2.{t^4}.{e^{ - 0,5t}})'} = 6,2.(4{t^3}.{e^{ - 0,5t}} + {t^4}.( - 0,5).{e^{ - 0,5t}})\\ = 24,8{t^3}.{e^{ - 0,5t}} - 3,1.{t^4}.{e^{ - 0,5t}}\end{array}\)

\({C'}(1) = 24,{8.1^3}.{e^{ - 0,5}} - 3,{1.1^4}.{e^{ - 0,5}} = 21,7.{e^{ - 0,5}} \approx 13,1617\)

b, \({C'}(5) = 24,{8.5^3}.{e^{ - 0,5.5}} - 3,{1.5^4}.{e^{ - 0,5.5}} \approx 95,4238\)

Vậy nồng độ tại thời điểm t=5 giây có nồng độ cao hơn.