 Toán 8, giải toán lớp 8 chân trời sáng tạo
Toán 8, giải toán lớp 8 chân trời sáng tạo
 Bài 2. Đường trung bình của tam giác Toán 8 chân trời s..
Bài 2. Đường trung bình của tam giác Toán 8 chân trời s..
Giải mục 2 trang 53 SGK Toán 8 tập 2– Chân trời sáng tạo
Cho
HĐ2
Video hướng dẫn giải
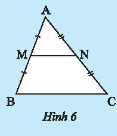
Cho \(M,N\) lần lượt là trung điểm của hai cạnh \(AB;AC\) của tam giác \(ABC\).
a) Tính các tỉ số \(\frac{{AM}}{{AB}},\frac{{AN}}{{AC}}\);
b) Cứng mình \(MN//BC\);
c) Chứng minh \(\frac{{MN}}{{BC}} = \frac{1}{2}\).
Phương pháp giải:
- Tỉ số giữa hai đoạn thẳng là tỉ số độ dài của hai đoạn thẳng khi cùng đơn vị đo.
- Định lí Thales đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
- Hệ quả định lí Thales
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải chi tiết:
a) Vì \(AM = MB \Rightarrow M\) là trung điểm của \(AB\) (do \(M\) thuộc \(AB\))
\( \Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}\);
Vì \(AN = NC \Rightarrow N\) là trung điểm của \(AC\) (do \(N\) thuộc \(AC\))
\( \Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}\).
b) Vì \(\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\).
Xét tam giác \(ABC\) có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) nên áp dụng định lí Thales đảo ta được \(MN//BC\).
c) Xét tam giác \(ABC\) có \(MN//BC\) nên áp dụng hệ quả định lí Thales ta được \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\).
Vậy \(\frac{{MN}}{{BC}} = \frac{1}{2}\) (điều phải chứng minh).
TH2
Video hướng dẫn giải
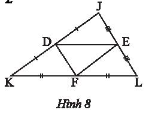
Trong Hình 8, cho biết \(JK = 10cm;DE = 6,5cm;EL = 3,7cm\). Tính \(DJ;EF;DF;KI\).
Phương pháp giải:
Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết:
Vì \(DJ = KD \Rightarrow D\) là trung điểm của \(JK\)
\( \Rightarrow DJ = DK = \frac{1}{2}JK = \frac{1}{2}.10 = 5cm\);
Vì \(EJ = EL \Rightarrow E\) là trung điểm của \(JL\).
\( \Rightarrow 2EL = JL \Leftrightarrow JL = 2.3,7 = 7,4cm\).
Vì \(KF = LF \Rightarrow F\) là trung điểm của \(KL\).
- Vì \(D\) là trung điểm của \(JK\); \(E\) là trung điểm của \(JL\) nên \(ED\) là đường trung bình của tam giác \(JLK\)\( \Rightarrow ED = \frac{1}{2}KL\) (tính chất đường trung bình)
Do đó, \(KL = 2ED = 2.6,5 = 13cm\);
- Vì \(E\) là trung điểm của \(JL\); \(F\) là trung điểm của \(KL\) nên \(EF\) là đường rung bình của tam giác \(JLK\)\( \Rightarrow EF = \frac{1}{2}JK\) (tính chất đường trung bình)
\( \Leftrightarrow EF = \frac{1}{2}.10 = 5cm\).
- Vì \(D\) là trung điểm của \(KJ\); \(F\) là trung điểm của \(KL\) nên \(DF\) là đường rung bình của tam giác \(JLK\)\( \Rightarrow DF = \frac{1}{2}JL\) (tính chất đường trung bình)
\( \Leftrightarrow DF = \frac{1}{2}.7,4 = 3,7cm\).
Vậy \(DJ = 5cm;EF = 5cm;DF = 3,7cm;KL = 13cm\)
VD2
Video hướng dẫn giải
Hãy tính khoảng cách \(BC\) trong phần câu hỏi khởi động trang 52.
Phương pháp giải:
- Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm của tam giác.
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết:
Vì \(BD = DA \Rightarrow D\) là trung điểm của \(AB\);
Vì \(EC = EA \Rightarrow E\) là trung điểm của \(AC\).
Do đó, \(DE\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right.\) (tính chất đường trung bình).
\( \Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)\)
Vậy khoảng các của hai điểm \(B\) và \(C\) là 90 m.
- Giải bài 1 trang 53 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 2 trang 54 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 3 trang 54 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 4 trang 54 SGK Toán 8 tập 2– Chân trời sáng tạo
- Giải bài 5 trang 54 SGK Toán 8 tập 2– Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo











