Giải mục 1 trang 8, 9, 10, 11 SGK Toán 11 tập 1 - Cùng khám phá
Trên đường tròn lượng giác, gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo \(\frac{{9\pi }}{4}\) và \( - \frac{\pi }{6}\). Tìm tọa độ của M và N.
Hoạt động 1
Trên đường tròn lượng giác, gọi M và N lần lượt là điểm biểu diễn của góc lượng giác có số đo \(\frac{{9\pi }}{4}\) và \( - \frac{\pi }{6}\). Tìm tọa độ của M và N.

Phương pháp giải:
Áp dụng công thức lượng giác:

Lời giải chi tiết:
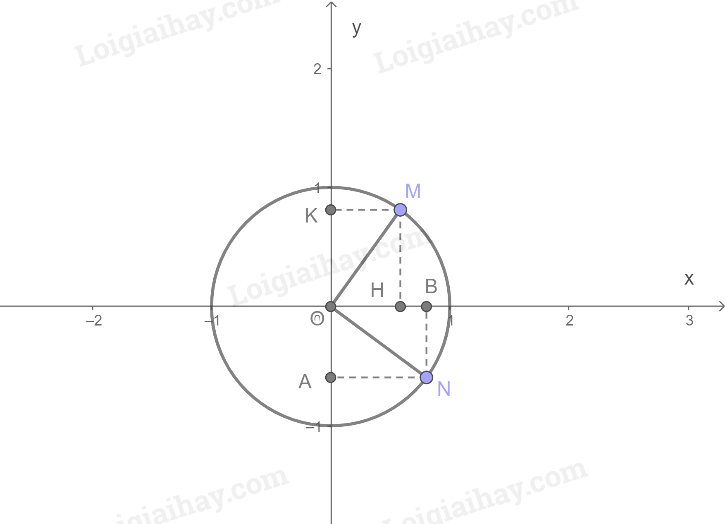
Gọi các điểm như trên hình vẽ
Gọi x và y lần lượt là hoành độ và tung độ của M \(\left( {x > 0,y > 0} \right)\)
Vì tam giác OMH vuông tại H và có góc \(\widehat {MOH} = \frac{\pi }{4}\) nên \(OH = OM.\cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\)
Vì tam giác OKM vuông tại K và có góc \(\widehat {MOK} = \frac{\pi }{4}\) nên \(OK = OM.\cos \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\).
Mà \(x > 0,y > 0\) nên \(M\left( {\frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\)
Gọi z và t là hoành độ và tung độ của N \(\left( {z > 0,t < 0} \right)\)
Vì tam giác OBN vuông tại B có góc \(\widehat {BON} = \frac{\pi }{6}\) nên \(OB = ON.\cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}\)
Vì tam giác OAN vuông tại A có góc \(\widehat {AON} = \frac{\pi }{3}\) nên \(OA = ON.\cos \frac{\pi }{3} = \frac{1}{2}\)
Mà \(z > 0,t < 0\) nên \(N\left( {\frac{{\sqrt 3 }}{2}; - \frac{1}{2}} \right)\).
Luyện tập 1
Tìm các giá trị lượng giác của góc 3300.
Phương pháp giải:
Áp dụng công thức lượng giác:
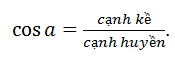
Lời giải chi tiết:

Trên đường tròn lượng giác, gọi M là điểm biểu diễn của góc lượng giác 3300
Gọi x và y lần lượt là hoành độ và tung độ của M. Ta có: \(x > 0,y < 0\)
Vì tam giác OMH vuông tại H và có góc \(\widehat {MOH} = {30^0}\) nên \(OH = OM.\cos {30^0} = \frac{{\sqrt 3 }}{2}\)
Vì tam giác OKM vuông tại K và có góc \(\widehat {MOK} = {60^0}\) nên \(OK = OM.\cos {60^0} = \frac{1}{2}\)
Suy ra: \(\cos {330^0} = x = \frac{{\sqrt 3 }}{2}\), \(\sin {330^0} = y = - \frac{1}{2}\)
\( \Rightarrow \tan {330^0} = \frac{{\sin {{330}^0}}}{{\cos {{330}^0}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = - \frac{{\sqrt 3 }}{3}\)
\( \Rightarrow \cot {330^0} = \frac{{\cos {{330}^0}}}{{\sin {{330}^0}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 \)
Hoạt động 2
Hãy viết lại bảng các giá trị lượng giác của một số góc đặc biệt từ 00 đến 900 đã học ở lớp 10.
Phương pháp giải:
Xem lại sách lớp 10
Lời giải chi tiết:
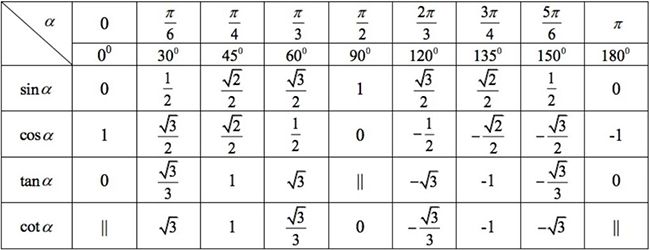
Luyện tập 2
Tính \(\sin \left( { - \frac{{35\pi }}{6}} \right),\cos \left( { - \frac{{35\pi }}{6}} \right),\tan \left( { - \frac{{35\pi }}{6}} \right),\cot \left( { - \frac{{35\pi }}{6}} \right)\).
Phương pháp giải:
\(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\end{array}\)
Lời giải chi tiết:
\(\begin{array}{l}\sin \left( { - \frac{{35\pi }}{6}} \right) = \sin \left( { - 6\pi + \frac{\pi }{6}} \right) = \sin \left( {\frac{\pi }{6}} \right) = \frac{1}{2}\\\cos \left( { - \frac{{35\pi }}{6}} \right) = \cos \left( { - 6\pi + \frac{\pi }{6}} \right) = \cos \left( {\frac{\pi }{6}} \right) = \frac{{\sqrt 3 }}{2}\\\tan \left( { - \frac{{35\pi }}{6}} \right) = \frac{{\sin \left( { - \frac{{35\pi }}{6}} \right)}}{{\cos \left( { - \frac{{35\pi }}{6}} \right)}} = \frac{{\sqrt 3 }}{3}\\\cot \left( { - \frac{{35\pi }}{6}} \right) = \frac{{\cos \left( { - \frac{{35\pi }}{6}} \right)}}{{\sin \left( { - \frac{{35\pi }}{6}} \right)}} = \sqrt 3 \end{array}\)
Luyện tập 3
Tính \(\sin {315^0},\cos \frac{{12\pi }}{7},\tan \left( { - {{168}^0}} \right)\).
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
\(\sin \left( {{{315}^0}} \right) = - \frac{{\sqrt 2 }}{2}\)
\(\cos \frac{{12\pi }}{7} \approx 0,62\)
\(\tan \left( { - {{168}^0}} \right) \approx 0,21\)
Vận dụng
Một cánh tay robot dài 1m được điều khiển để gắp một vật tại điểm C, rồi xoay theo chiều dương một góc 2250 để thả vật tại điểm D như Hình 1.20. Chọn hệ trục tọa độ Oxy sao cho tâm của cánh tay robot trùng với O và C có tọa độ là (1; 0). Tìm tọa độ của vật tại điểm D.
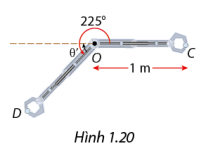
Phương pháp giải:
Hoành độ của điểm D là \(\cos {225^0}\), tung độ của điểm D là \(\sin {225^0}\).
Lời giải chi tiết:

Gọi x và y là hoành độ và tung độ của D
\(\begin{array}{l}x = \cos {225^0} = - \frac{{\sqrt 2 }}{2}\\y = \sin {225^0} = - \frac{{\sqrt 2 }}{2}\end{array}\)
Vậy \(D\left( { - \frac{{\sqrt 2 }}{2}; - \frac{{\sqrt 2 }}{2}} \right)\).
Các bài khác cùng chuyên mục
- Bài 4.20 trang 114 SGK Toán 11 tập 1 - Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá













Danh sách bình luận