Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều
Bài 3. Biểu thức tọa độ của các phép toán vecto - Toán ..
Giải mục 1 trang 74,75 SGK Toán 12 tập 1 - Cánh diều
Biểu thức tọa độ của phép cộng hai vecto, phép trừ hai vecto, phép nhân một số với một vecto
Đề bài
Trả lời câu hỏi Hoạt động 1 trang 74 SGK Toán 12 Cánh diều
Trong không gian với hệ tọa độ Oxyz (Hình 36), cho hai vecto \(\overrightarrow u = ({x_1};{y_1};{z_1})\) và \(\overrightarrow v = ({x_2};{y_2};{z_2})\).
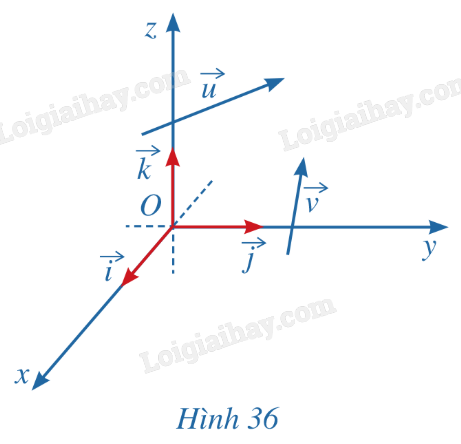
a) Biểu diễn các vecto \(\overrightarrow u ,\overrightarrow v \) theo ba vecto \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \)
b) Biểu diễn các vecto \(\overrightarrow u + \overrightarrow v \), \(\overrightarrow u - \overrightarrow v \), \(m\overrightarrow u (m \in \mathbb{R})\) theo ba vecto \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \)
c) Tìm tọa độ các vecto \(\overrightarrow u + \overrightarrow v \), \(\overrightarrow u - \overrightarrow v \), \(m\overrightarrow u (m \in \mathbb{R})\)
Phương pháp giải - Xem chi tiết
\(\overrightarrow i = (1;0;0);\overrightarrow j = (0;1;0);\overrightarrow k = (0;0;1)\). Áp dụng quy tắc nhân vecto với một số và quy tắc cộng trừ 2 vecto
Lời giải chi tiết
a) \(\overrightarrow u = ({x_1};{y_1};{z_1}) = {x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k \)
\(\overrightarrow v = ({x_2};{y_2};{z_2}) = {x_2}\overrightarrow i + {y_2}\overrightarrow j + {z_2}\overrightarrow k \)
b) \(\overrightarrow u + \overrightarrow v = {x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k + {x_2}\overrightarrow i + {y_2}\overrightarrow j + {z_2}\overrightarrow k = ({x_1} + {x_2})\overrightarrow i + ({y_1} + {y_2})\overrightarrow j + ({z_1} + {z_2})\overrightarrow k \)
\(\overrightarrow u - \overrightarrow v = {x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k - {x_2}\overrightarrow i - {y_2}\overrightarrow j - {z_2}\overrightarrow k = ({x_1} - {x_2})\overrightarrow i + ({y_1} - {y_2})\overrightarrow j + ({z_1} - {z_2})\overrightarrow k \)
\(m\overrightarrow u = m({x_1}\overrightarrow i + {y_1}\overrightarrow j + {z_1}\overrightarrow k ) = m{x_1}\overrightarrow i + m{y_1}\overrightarrow j + m{z_1}\overrightarrow k \)
c) \(\overrightarrow u + \overrightarrow v = ({x_1} + {x_2})\overrightarrow i + ({y_1} + {y_2})\overrightarrow j + ({z_1} + {z_2})\overrightarrow k = ({x_1} + {x_2};{y_1} + {y_2};{z_1} + {z_2})\)
\(\overrightarrow u - \overrightarrow v = ({x_1} - {x_2})\overrightarrow i + ({y_1} - {y_2})\overrightarrow j + ({z_1} - {z_2})\overrightarrow k = ({x_1} - {x_2};{y_1} - {y_2};{z_1} - {z_2})\)
\(m\overrightarrow u = m{x_1}\overrightarrow i + m{y_1}\overrightarrow j + m{z_1}\overrightarrow k = (m{x_1};m{y_1};m{z_1})\)
Bình luận
Chia sẻ
- Giải mục 2 trang 75,76 SGK Toán 12 tập 1 - Cánh diều
- Giải mục 3 trang 76,77,78 SGK Toán 12 tập 1 - Cánh diều
- Giải mục 4 trang 79,80 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 1 trang 80 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 2 trang 80 SGK Toán 12 tập 1 - Cánh diều
>> Xem thêm
