 Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều
Toán 12 Cánh diều | Giải toán lớp 12 Cánh diều
 Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số -..
Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số -..
Giải mục 1 trang 28, 29 SGK Toán 12 tập 1 - Cánh diều
Sơ đồ khảo sát hàm số
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
HĐ
Trả lời câu hỏi Hoạt động trang 28 SGK Toán 12 Cánh diều
Lập bảng biến thiên và vẽ đồ thị của hàm số \(y = {x^2} - 2x - 3\).
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
- Tập xác định: \(\mathbb{R}\).
- Sự biến thiên:
Giới hạn tại vô cực : \(\mathop {\lim }\limits_{x \to + \infty } = - \infty \); \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty \);
Ta có \(y{\rm{'}} = 2x - 2\).
\(y{\rm{'}} = 0 \Leftrightarrow 2x - 2 = 0 \Leftrightarrow x = 1\).
Bảng biến thiên:
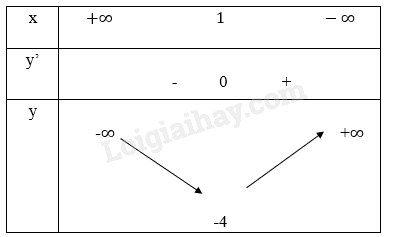
Vẽ đồ thị hàm số:
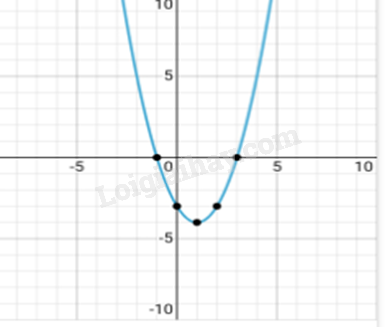
LT1
Trả lời câu hỏi Luyện tập 1 trang 29 SGK Toán 12 Cánh diều
Khảo sát và sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{x - 1}}{{x + 1}}\).
Phương pháp giải:
- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Lời giải chi tiết:
Lời giải
1) TXĐ: \(D = \mathbb{R}\backslash \{ - 1\} \).
2) Sự biến thiên:
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận:
\(\mathop {\lim }\limits_{x \to - {1^ - }} y = + \infty \); \(\mathop {\lim }\limits_{x \to - {1^ + }} y = - \infty \). Do đó, đường thẳng x = -1 là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } y = 1\); \(\mathop {\lim }\limits_{x \to - \infty } y = 1\). Do đó, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
Đạo hàm: \(y' = \frac{2}{{{{(x + 1)}^2}}} > 0\), với mọi \(x \ne - 1\).
Bảng biến thiên:
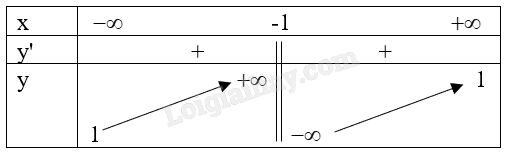
Hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( { - 1; + \infty } \right)\).
Hàm số không có cực trị.
3) Đồ thị:
- Giao điểm của đồ thị với trục tung: (0;-1).
- Giao điểm của đồ thị với trục hoành: (1;0).
- Đồ thị hàm số đi qua các điểm (0;-1), (1;0), (-2;3) và (-3;2).
- Đồ thị hàm số nhận giao điểm (-1;1) của hai đường tiệm cận của đồ thị làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Ta vẽ được đồ thị \(y = \frac{{x - 1}}{{x + 1}}\) như hình:
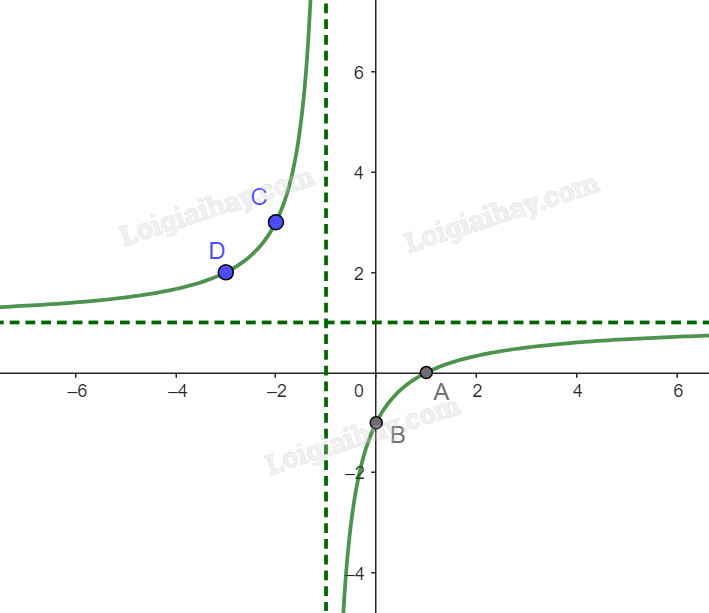
- Giải mục 2 trang 30 SGK Toán 12 tập 1 - Cánh diều
- Giải mục 3 trang 31, 32, 34, 35 SGK Toán 12 tập 1 - Cánh diều
- Giải mục 4 trang 41 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 1 trang 42 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 2 trang 42 SGK Toán 12 tập 1 - Cánh diều
>> Xem thêm
Các bài khác cùng chuyên mục











