-
Vở thực hành Toán 9 - Tập 1
-
Chương I. Phương trình và hệ hai phương trình bậc nhất hai ẩn
-
Chương II. Phương trình và bất phương trình bậc nhất một ẩn
-
Chương III. Căn bậc hai và căn bậc ba
-
Chương IV. Hệ thức lượng trong tam giác vuông
-
Chương V. Đường tròn
- Bài 13. Mở đầu về đường tròn
- Bài 14. Cung và dây của một đường tròn
- Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
- Luyện tập chung trang 107
- Bài 16. Vị trí tương đối của đường thẳng và đường tròn
- Bài 17. Vị trí tương đối của hai đường tròn
- Luyện tập chung trang 119
- Bài tập cuối chương V
-
-
Vở thực hành Toán 9 - Tập 2
Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
Bài tập cuối chương VI trang 33, 34, 35 Vở thực hành To..
Giải câu hỏi trắc nghiệm trang 33 vở thực hành Toán 9 tập 2
Điểm nào sau đây thuộc đồ thị của hàm số (y = frac{1}{2}{x^2})? A. (left( {1;2} right)). B. (left( {2;1} right)). C. (left( {2;1} right)). D. (left( { - 1;frac{1}{2}} right)).
Chọn phương án đúng trong mỗi câu sau:
Câu 1
Trả lời Câu 1 trang 33 Vở thực hành Toán 9
Điểm nào sau đây thuộc đồ thị của hàm số \(y = \frac{1}{2}{x^2}\)?
A. \(\left( {1;2} \right)\).
B. \(\left( {2;1} \right)\).
C. \(\left( {2;1} \right)\).
D. \(\left( { - 1;\frac{1}{2}} \right)\).
Phương pháp giải:
Thay \(x = - 1\) vào đồ thị hàm số \(y = \frac{1}{2}{x^2}\), tìm được \(y = \frac{1}{2}\) nên tìm được điểm thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
Lời giải chi tiết:
Với \(x = - 1\), thay vào hàm số \(y = \frac{1}{2}{x^2}\) ta có: \(y = \frac{1}{2}.{\left( { - 1} \right)^2} = \frac{1}{2}\). Do đó, điểm \(\left( { - 1;\frac{1}{2}} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{2}{x^2}\).
Chọn D
Câu 2
Trả lời Câu 2 trang 33 Vở thực hành Toán 9
Hình bên là hai đường parabol trong mặt phẳng tọa độ Oxy. Khẳng định nào sau đây là đúng?
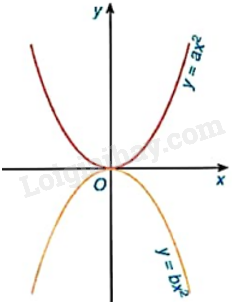
A. \(a < 0 < b\).
B. \(a < b < 0\).
C. \(a > b > 0\).
D. \(a > 0 > b\).
Phương pháp giải:
Đồ thị hàm số: \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Nằm phía trên trục hoành nếu \(a > 0\).
+ Nằm phía dưới trục hoành nếu \(a < 0\).
Lời giải chi tiết:
Vì đồ thị hàm số \(y = b{x^2}\) nằm phía dưới trục hoành nên \(0 > b\).
Vì đồ thị hàm số \(y = a{x^2}\) nằm phía trên trục hoành nên \(a > 0\).
Do đó, \(a > 0 > b\).
Chọn D
Câu 3
Trả lời Câu 3 trang 33 Vở thực hành Toán 9
Các nghiệm của phương trình \({x^2} + 7x + 12 = 0\) là
A. \({x_1} = 3;{x_2} = 4\).
B. \({x_1} = - 3;{x_2} = - 4\).
C. \({x_1} = 3;{x_2} = - 4\).
D. \({x_1} = - 3;{x_2} = 4\).
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Tính biệt thức \(\Delta = {b^2} - 4ac\).
+ Nếu \(\Delta > 0\) thì phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}}\).
+ Nếu \(\Delta = 0\) thì phương trình có nghiệm kép: \({x_1} = {x_2} = \frac{{ - b}}{{2a}}\).
+ Nếu \(\Delta < 0\) thì phương trình vô nghiệm.
Lời giải chi tiết:
Vì \(\Delta = {7^2} - 4.1.12 = 1 > 0\) nên phương trình có hai nghiệm phân biệt: \({x_1} = \frac{{ - 7 + 1}}{2} = - 3;{x_2} = \frac{{ - 7 - 1}}{2} = - 4\)
Chọn B
Câu 4
Trả lời Câu 4 trang 33 Vở thực hành Toán 9
Phương trình bậc hai có hai nghiệm \({x_1} = 13\) và \({x_2} = 25\) là
A. \({x^2} - 13x + 25 = 0\).
B. \({x^2} - 25x + 13 = 0\).
C. \({x^2} - 38x + 325 = 0\).
D. \({x^2} + 38x + 325 = 0\).
Phương pháp giải:
Hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình \({x^2} - Sx + P = 0\) (điều kiện \({S^2} - 4P \ge 0\)).
Lời giải chi tiết:
Tổng hai nghiệm của phương trình là \(S = 38,\) tích hai nghiệm của phương trình là \(P = 325\) nên \({x_1},{x_2}\) là hai nghiệm của phương trình: \({x^2} - 38x + 325 = 0\).
Chọn C
Câu 5
Trả lời Câu 5 trang 33 Vở thực hành Toán 9
Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \({x^2} - 5x + 6 = 0\). Khi đó giá trị của biểu thức \(A = x_1^2 + x_2^2\) là
A. 13.
B. 19.
C. 25.
D. 5.
Phương pháp giải:
Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\).
+ Tính biệt thức \(\Delta = {b^2} - 4ac\).
+ Nếu \(\Delta > 0\) thì áp dụng định lí Viète để tính tổng và tích các nghiệm \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}.{x_2} = \frac{c}{a}\).
Biến đổi \(x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}\), từ đó thay \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}.{x_2} = \frac{c}{a}\) để tính giá trị biểu thức.
Lời giải chi tiết:
Vì \(\Delta = {\left( { - 5} \right)^2} - 4.6 = 1 > 0\) nên phương trình có hai nghiệm phân biệt.
Theo định lí Viète ta có: \({x_1} + {x_2} = 5;{x_1}.{x_2} = 6\)
Ta có: \(A = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = {5^2} - 2.6 = 13\)
Chọn A
Câu 6
Trả lời Câu 6 trang 33 Vở thực hành Toán 9
Chiều dài và chiều rộng của hình chữ nhật có chu vi 20cm và diện tích \(24c{m^2}\) là
A. 5cm và 4cm.
B. 6cm và 4cm.
C. 8cm và 3cm.
D. 10cm và 2cm.
Phương pháp giải:
+ Chiều dài và chiều rộng là nghiệm của phương trình \({x^2} - 10x + 24 = 0\).
+ Sử dụng công thức nghiệm thu gọn để tìm x, từ đó kết luận.
Lời giải chi tiết:
Nửa chu vi hình chữ nhật là: \(20:2 = 10\left( {cm} \right)\)
Chiều dài và chiều rộng là nghiệm của phương trình: \({x^2} - 10x + 24 = 0\)
Vì \(\Delta ' = {\left( { - 5} \right)^2} - 24 = 1 > 0\) nên phương trình có hai nghiệm phân biệt: \({x_1} = 5 + 1 = 6;{x_2} = 5 - 1 = 4\).
Do đó, chiều dài và chiều rộng của hình chữ nhật lần lượt là 6cm và 4cm (do chiều dài > chiều rộng).
Chọn B
Bình luận
Chia sẻ
- Giải bài 1 trang 34 vở thực hành Toán 9 tập 2
- Giải bài 2 trang 35 vở thực hành Toán 9 tập 2
- Giải bài 3 trang 35 vở thực hành Toán 9 tập 2
- Giải bài 4 trang 35, 36 vở thực hành Toán 9 tập 2
- Giải bài 5 trang 36 vở thực hành Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
