Giải câu hỏi trắc nghiệm trang 132, 133 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Câu 1

Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?

A. Ba điểm.

B. Một điểm và một đường thẳng.

C. Hai đường thẳng cắt nhau.

D. Bốn điểm.

Phương pháp giải:

Sử dụng kiến thức về cách xác định mặt phẳng để tìm đáp án đúng: Một mặt phẳng được xác định nếu biết nó chứa hai đường thẳng cắt nhau.

Lời giải chi tiết:

Một mặt phẳng được xác định nếu biết nó chứa hai đường thẳng cắt nhau nên đáp án C đúng.

A sai vì ba điểm đó cần thêm điều kiện không thẳng hàng.

B sai vì thiếu điều kiện điểm không thuộc đường thẳng đó.

D sai vì qua 4 điểm thẳng hàng thì không xác định được một mặt phẳng.

Chọn C

Câu 2

Cho hình chóp S. ABCD có đáy ABCD là hình thang, đáy lớn AB và E là trung điểm của đoạn thẳng AB. Hình vẽ nào sau đây là hình biểu diễn của hình chóp S. ABCD?

A.

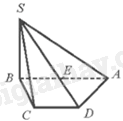
B.

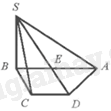
C.

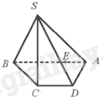
D.

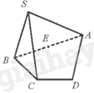
Phương pháp giải:

Sử dụng kiến thức về hình biểu diễn của một hình trong không gian để tìm hình biểu diễn: Hình biểu diễn của một hình H trong không gian là hình chiếu song song của H trên mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.

Lời giải chi tiết:

Hình biểu diễn đúng là:

Chọn A.

Câu 3

Cho hình chóp S. ABCD có AC cắt BD tại M, AB cắt CD tại N. Trong các đường thẳng sau đây, đường thẳng nào là giao tuyến của (SAC) và (SBD)?

A. SM.

B. SN.

C. SB.

D. SC.

Phương pháp giải:

Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến: Đường thẳng d chung giữa hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).

Lời giải chi tiết:

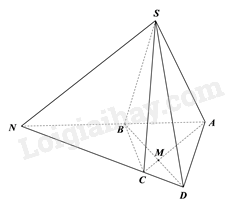
Vì M thuộc AC, mà \(AC \subset \left( {SAC} \right) \Rightarrow M \in \left( {SAC} \right)\).

Vì M thuộc BD, mà \(BD \subset \left( {SBD} \right) \Rightarrow M \in \left( {SBD} \right)\).

Lại có: \(S \in \left( {SAC} \right) \cap \left( {SBD} \right)\) nên giao tuyến của (SAC) và (SBD) là SM.

Chọn A

Câu 4

Cho hình chóp S. ABCD, đáy là hình bình hành có O là giao điểm của AC và BD. Gọi M, N lần lượt là các điểm nằm trên cạnh SC và SD. Đường thẳng SO cắt đường thẳng AM và BN lần lượt tại P và Q. Giao điểm của đường thẳng AM với mặt phẳng (SBD) là điểm nào sau đây?

A. Điểm P.

B. Điểm Q.

C. Điểm O.

D. Điểm M.

Phương pháp giải:

Sử dụng kiến thức về giao điểm giữa đường thẳng và mặt phẳng để tìm giao tuyến: Cách tìm giao điểm của đường thẳng d và mặt phẳng \(\left( \alpha  \right)\):

- Trường hợp 1: Trong mặt phẳng \(\left( \alpha  \right)\) có sẵn đường thẳng d’ cắt d tại I: Ta có ngay \(d \cap \left( \alpha  \right) = I\)

- Trường hợp 2: Trong mặt phẳng \(\left( \alpha  \right)\) không có sẵn đường thẳng d’ cắt d. Khi đó ta thực hiện như sau:

+ Chọn mặt phẳng phụ \(\left( \beta  \right)\) chứa d và \(\left( \beta  \right)\) cắt \(\left( \alpha  \right)\) theo giao tuyến d’.

+ Gọi \(I = d' \cap d\). Khi đó, \(d \cap \left( \alpha  \right) = I\).

Lời giải chi tiết:

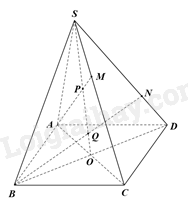
Vì P là giao điểm của AM và SO, mà \(SO \subset \left( {SBD} \right)\) nên P là giao điểm của AM và mặt phẳng (SBD).

Chọn A

Câu 5

Trong không gian, hai đường thẳng không có điểm chung thì

A. cắt nhau.

B. chéo nhau hoặc song song.

C. chéo nhau.

D. song song.

Phương pháp giải:

Sử dụng kiến thức về vị trí tương đối của hai đường thẳng trong không gian: Trong không gian, hai đường thẳng không có điểm chung thì chéo nhau hoặc song song.

Lời giải chi tiết:

Trong không gian, hai đường thẳng không có điểm chung thì chéo nhau hoặc song song.

Chọn B

Câu 6

Cho hai đường thẳng song song a, b và mặt phẳng (P). Mệnh đề nào dưới đây đúng?

A. Nếu a//(P) thì b//(P).

B. Nếu a cắt (P) thì b cắt (P).

C. Nếu a nằm trên (P) thì b//(P).

D. Nếu a nằm trên (P) thì b nằm trên (P).

Phương pháp giải:

Sử dụng kiến thức về đường thẳng song song với mặt phẳng để tìm mệnh đề đúng: Cho hai đường thẳng song song a, b. Nếu a cắt (P) thì b cắt (P).

Lời giải chi tiết:

Câu đúng: Cho hai đường thẳng song song a, b. Nếu a cắt (P) thì b cắt (P).

Câu A sai vì: Nếu a//b, a//(P) thì b//(P) hoặc b nằm trong (P).

Câu C, D sai vì: Nếu a//b, a nằm trên (P) thì b//(P) hoặc b nằm trong (P).

Chọn B

Câu 7

Cho tứ diện ABCD có P, Q lần lượt là trọng tâm của tam giác ABC và BCD. Giao tuyến của mặt phẳng (ABQ) và mặt phẳng (DCP) là đường thẳng d. Khẳng định nào dưới đây đúng?

A. d đi qua trung điểm hai cạnh AB và CD.

B. d đi qua trung điểm hai cạnh AB và AD.

C. d là đường thẳng PQ.

D. d là đường thẳng QA.

Phương pháp giải:

Sử dụng kiến thức về giao tuyến giữa hai mặt phẳng để tìm giao tuyến: Đường thẳng d chung giữa hai mặt phẳng (P) và (Q) được gọi là giao tuyến của (P) và (Q), kí hiệu  \(d = \left( P \right) \cap \left( Q \right)\).

Lời giải chi tiết:

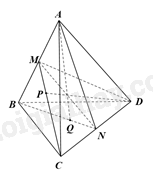
Gọi M, N lần lượt là trung điểm của AB, CD.

Vì \(M \in AB,AB \subset \left( {ABQ} \right) \Rightarrow M \in \left( {ABQ} \right)\) (1)

Khi đó, trung tuyến CM đi qua trọng tâm P của tam giác ABC.

Vì \(M \in PC,PC \subset \left( {DCP} \right) \Rightarrow M \in \left( {DCP} \right)\) (2)

Từ (1) và (2) ta có: \(M \in \left( {ABQ} \right) \cap \left( {DCP} \right)\).

Chứng minh tương tự ta có: \(N \in \left( {ABQ} \right) \cap \left( {DCP} \right)\).

Do đó, MN là giao tuyến của mặt phẳng (ABQ) và mặt phẳng (DCP).

Chọn A

Câu 8

Cho hình chóp tứ giác S. ABCD. Gọi M và N lần lượt là trung điểm của SA và SC. Khẳng định nào sau đây đúng?

A. MN//(ABCD).

B. MN//(SAB).

C. MN//(SAD).

D. MN//(SCD).

Phương pháp giải:

Sử dụng kiến thức về điều kiện để một đường thẳng song song với một mặt phẳng để chứng minh: Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P). 

Lời giải chi tiết:

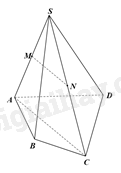
Vì M và N lần lượt là trung điểm của SA và SC nên MN là đường trung bình của tam giác SAC. Do đó, MN//AC.

Mà \(AC \subset \left( {ABCD} \right)\), MN không nằm trong mặt phẳng (ABCD) nên MN//(ABCD).

Chọn A

Câu 9

Cho đường thẳng a nằm trong mặt phẳng \(\left( \alpha  \right)\) và đường thẳng b nằm trong mặt phẳng \(\left( \beta  \right)\). Biết \(\left( \alpha  \right)//\left( \beta  \right)\). Trong các khẳng định sau, khẳng định nào sai?

A. a//\(\left( \beta  \right)\).

B. b//\(\left( \alpha  \right)\).

C. a//b.

D. Nếu có một mặt phẳng \(\left( \gamma  \right)\) chứa a và b thì a//b.

Phương pháp giải:

Sử dụng kiến thức về hai mặt phẳng song song để tìm khẳng định sai: Nếu \(a \subset \left( \alpha  \right),b \subset \left( \beta  \right),\) \(\left( \alpha  \right)//\left( \beta  \right)\) thì a//b hoặc a và b chéo nhau. 

Lời giải chi tiết:

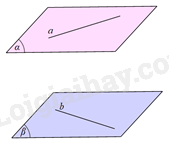
Nếu \(a \subset \left( \alpha  \right),b \subset \left( \beta  \right),\) \(\left( \alpha  \right)//\left( \beta  \right)\) thì a//b hoặc a và b chéo nhau nên C sai.

Chọn C

Câu 10

Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với đường thẳng nào sau đây?

A. BD.

B. SC.

C. AC.

D. AB.

Phương pháp giải:

Sử dụng kiến thức về tính chất cơ bản về hai đường thẳng song song để chứng minh: Nếu hai mặt phẳng phân biệt lần lượt đi qua hai đường thẳng song song thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.

Lời giải chi tiết:

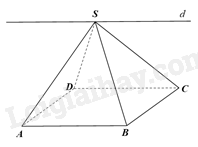
Vì ABCD là hình bình hành nên AB//CD.

Mà \(AB \subset \left( {SAB} \right),CD \subset \left( {SCD} \right),S \in \left( {SAB} \right) \cap \left( {SCD} \right)\) nên giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng d đi qua S song song với AB, CD.

Chọn D