Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 1 - Chân trời sáng tạo

Có thể tính phương sai và độ lệch chuẩn của số liệu ở biểu đồ trên hay không?

Tổng hợp đề thi giữa kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Có thể tính phương sai và độ lệch chuẩn của số liệu ở biểu đồ trên hay không?

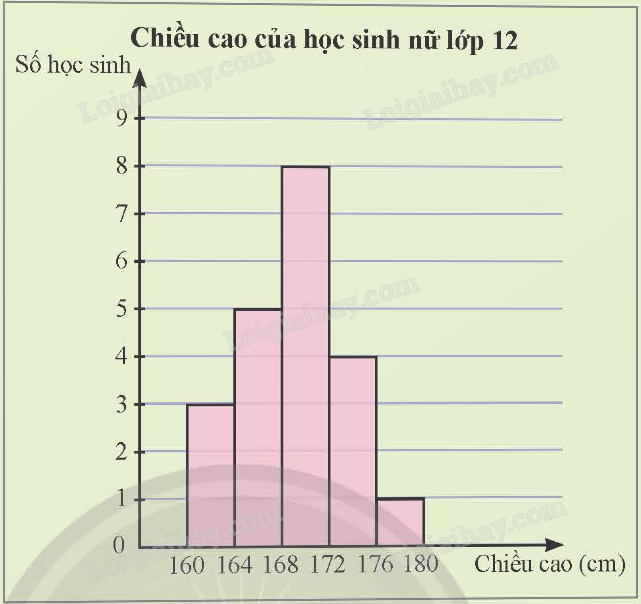
Phương pháp giải - Xem chi tiết

Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:

\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)

Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu

\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình

Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.

Lời giải chi tiết

Cỡ mẫu: n = 21.

Giá trị trung bình của mẫu số liệu mới:

\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}) \)

\(= \frac{1}{{21}}(3.162 + 5.166 + 8.170 + 4.174 + 1.178)\)

\(= \frac{{3550}}{{21}}\).

Phương sai của mẫu số liệu mới:

\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}] \)

\(= \frac{1}{{21}}[3{(162 - \frac{{3550}}{{21}})^2} + 5{(166 - \frac{{3550}}{{21}})^2} + ... + 1{(178 - \frac{{3550}}{{21}})^2}]\)

\(= \frac{{8000}}{{441}}\).

Độ lệch chuẩn của mẫu số liệu mới:

\(\sigma = \sqrt {{S^2}} = \sqrt {\frac{{8000}}{{441}}} = \frac{{40\sqrt 5 }}{{21}}\).

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 4 phiếu

Bài tiếp theo

Giải trang 75, 82 SGK Toán 12 tập 1 - Chân trời sáng tạo
Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm
Giải bài tập 1 trang 82 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bảng dưới đây thống kê cự li ném tạ của một vận động viên. Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
Giải bài tập 2 trang 82 SGK Toán 12 tập 1 - Chân trời sáng tạo
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được mô tả bằng biểu đồ bên. a) Hãy cho biết có bao nhiêu máy vi tính có thời gian sử dụng pin từ 7,2 đến dưới 7,4 giờ? b) Hãy xác định số trung bình và độ lệch chuẩn của thời gian sử dụng pin.
Giải bài tập 3 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tốc độ của 20 xe hơi khi đi qua một trạm kiểm tra tốc độ (đơn vị: km/h) được thống kê lại như sau: a) Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên. b) Hãy lập bảng tần số ghép nhóm với nhóm đầu tiên là [42; 46) và độ dài mỗi nhóm bằng 4. c) Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu ghép nhóm.
Giải bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo
Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau: a) Hãy so sánh đường kính trung bình của thân cây xoan đào trồng tại địa điểm A và địa điểm B. b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?
Lý thuyết Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm Toán 12 Chân trời sáng tạo
Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm 1. Phương sai và độ lệch chuẩn