Giải câu hỏi mở đầu trang 68 SGK Toán 12 tập 1 - Chân trời sáng tạo

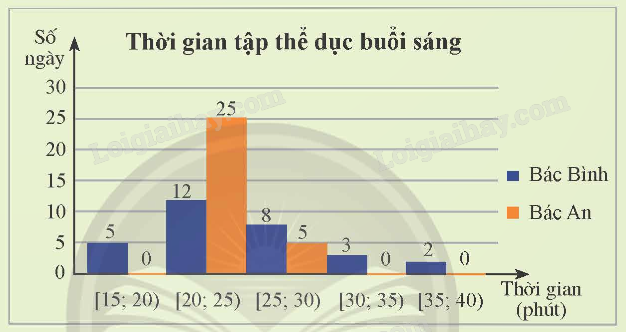
Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An. Ai là người có thời gian tập đều hơn?

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.

Ai là người có thời gian tập đều hơn?

Phương pháp giải - Xem chi tiết

Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).

Quảng cáo

Lời giải chi tiết

Từ biểu đồ đã cho, ta có bảng thống kê sau:

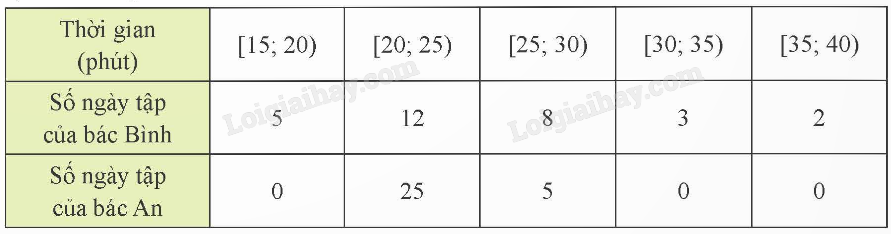
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác Bình là 40 – 15 = 25 (phút).

Tuy nhiên, trong mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An, khoảng đầu tiên chứa dữ liệu là [20; 25) và khoảng cuối cùng chứa dữ liệu là [25; 30). Do đó, khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng của bác An là 30 – 20 = 10 (phút).

Nếu căn cứ theo khoảng biến thiên thì bác Bình có thời gian tập thể dục phân tán hơn bác An, vậy bác An là người có thời gian tập đều hơn.

Cỡ mẫu \(n = 30\).

Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác An được xếp theo thứ tự không giảm.

Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{25}} \in [20;25)\); \({x_{26}}; \ldots ;{\rm{ }}{x_{30}} \in [25;30)\);

Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

\({Q_1} = 20 + \frac{{\frac{{30}}{4}}}{{25}}(25 - 20) = \frac{{43}}{2}\).

Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{23}} \in [20;25)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

\({Q_3} = 20 + \frac{{\frac{{3.30}}{4}}}{{25}}(25 - 20) = \frac{{49}}{2}\).

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 3\).

Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình được xếp theo thứ tự không giảm.

Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_5} \in [15;20)\); \({y_6}; \ldots ;{\rm{ }}{y_{17}} \in [20;25)\);\({y_{18}}; \ldots ;{\rm{ }}{y_{25}} \in [25;30)\);\({y_{26}};{y_{27}};{\rm{ }}{y_{28}} \in [30;35)\);\({y_{29}};{y_{30}} \in [35;40)\).

Tứ phân vị thứ nhất của mẫu số liệu gốc là \({y_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

\({Q_1}' = 20 + \frac{{\frac{{30}}{4}}-5}{{12}}(25 - 20) = \frac{{505}}{24}\).

Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{23}} \in [25;30)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

\({Q_3}' = 25 + \frac{{\frac{{3.30}}{4} - (5 + 12)}}{8}(30 - 25) = \frac{{455}}{{16}}\).

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

\({\Delta _Q}' = {Q_3}' - {Q_1}' = \frac{{355}}{{48}}\).

Vì \(\frac{{355}}{{48}}>3\) nên khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn bác An.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 68, 69, 70 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khoảng biến thiên
Giải mục 2 trang 70, 71, 72 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khoảng tứ phân vị
Giải bài tập 1 trang 73 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bảng sau thống kê tổng lượng mưa (đơn vị: mm) đo được vào tháng 7 từ năm 2002 đến 2021 tại một trạm quan trắc đặt ở Cà Mau. a) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu trên. b) Hãy chia mẫu số liệu trên thành 4 nhóm với nhóm đầu tiên là [140; 240) và lập bảng tần số ghép nhóm. c) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm và so sánh với kết quả tương ứng thu được ở câu a).
Giải bài tập 2 trang 74 SGK Toán 12 tập 1 - Chân trời sáng tạo
Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn; … Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên.
Giải bài tập 3 trang 74 SGK Toán 12 tập 1 - Chân trời sáng tạo
Kết quả đo chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được cho ở bảng sau: a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên. b) Trong 100 cây keo trên có 1 cây cao 8,4 m. Hỏi chiều cao của cây keo này có phải là giá trị ngoại lệ không?
Giải bài tập 4 trang 74 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bảng tần số ghép nhóm dưới đây thể hiện kết quả điều tra về tuổi thọ trung bình của nam giới và nữ giới ở 50 quốc gia. a) Hãy tính các khoảng tứ phân vị của tuổi thọ trung bình của nam giới và nữ giới trong mẫu số liệu ghép nhóm trên. b) Hãy cho biết tuổi thọ trung bình của nam giới hay nữ giới trong mẫu số liệu ghép nhóm trên đồng đều hơn.
Lý thuyết Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm Toán 12 Chân trời sáng tạo
Bài 1. Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm 1. Khoảng biến thiên