Giải bài tập 2 trang 74 SGK Toán 12 tập 1 - Chân trời sáng tạo

Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn; … Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên.

Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa

Đề bài

Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn; …

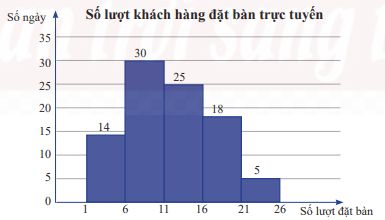
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên.

Phương pháp giải - Xem chi tiết

Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:

\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)

trong đó:

\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu

\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k

\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k

\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)

Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).

Lời giải chi tiết

Cỡ mẫu \(n = 92\);

Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{92}}\) là mẫu số liệu gốc về số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của nhà hàng được xếp theo thứ tự không giảm.

Ta có: \({x_1};...{\rm{; }}{x_{14}} \in [1;6)\); \({x_{15}}; \ldots ;{\rm{ }}{x_{44}} \in [6;11)\);\({x_{45}}; \ldots ;{\rm{ }}{x_{69}} \in [11;16)\);\({x_{70}}; \ldots ;{\rm{ }}{x_{87}} \in [16;21)\);\({x_{88}}; \ldots ;{\rm{ }}{x_{92}} \in [21;26)\)

Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_{23}} + {x_{24}}) \in [6;11)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 6 + \frac{{\frac{{92}}{4} - 14}}{{30}}(11 - 6) = 7,5\)

Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({x_{69}} + {x_{70}}) \in [11;16)\)và \([16;21)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 16\)

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 8,5\)

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 7 phiếu

Bài tiếp theo

Giải bài tập 3 trang 74 SGK Toán 12 tập 1 - Chân trời sáng tạo
Kết quả đo chiều cao của 100 cây keo 3 năm tuổi tại một nông trường được cho ở bảng sau: a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm trên. b) Trong 100 cây keo trên có 1 cây cao 8,4 m. Hỏi chiều cao của cây keo này có phải là giá trị ngoại lệ không?
Giải bài tập 4 trang 74 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bảng tần số ghép nhóm dưới đây thể hiện kết quả điều tra về tuổi thọ trung bình của nam giới và nữ giới ở 50 quốc gia. a) Hãy tính các khoảng tứ phân vị của tuổi thọ trung bình của nam giới và nữ giới trong mẫu số liệu ghép nhóm trên. b) Hãy cho biết tuổi thọ trung bình của nam giới hay nữ giới trong mẫu số liệu ghép nhóm trên đồng đều hơn.
Giải bài tập 1 trang 73 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bảng sau thống kê tổng lượng mưa (đơn vị: mm) đo được vào tháng 7 từ năm 2002 đến 2021 tại một trạm quan trắc đặt ở Cà Mau. a) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu trên. b) Hãy chia mẫu số liệu trên thành 4 nhóm với nhóm đầu tiên là [140; 240) và lập bảng tần số ghép nhóm. c) Hãy tìm khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm và so sánh với kết quả tương ứng thu được ở câu a).
Giải mục 2 trang 70, 71, 72 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khoảng tứ phân vị
Giải mục 1 trang 68, 69, 70 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khoảng biến thiên
Lý thuyết Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm Toán 12 Chân trời sáng tạo
Bài 1. Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm 1. Khoảng biến thiên