Giải bài tập 9.30 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức

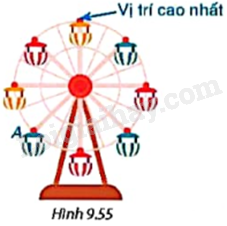
Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?

Đề bài

Cho vòng quay mặt trời gồm tám cabin như Hình 9.55. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều kim đồng hồ quanh tâm bao nhiêu độ?

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

+ Gọi tám cabin tạo thành một bát giác đều BACDEFGH nội tiếp đường tròn (O).

+ Chứng minh \(\Delta HOB = \Delta HOG = \Delta FOG = \Delta FOE = \Delta DOE = \Delta DOC = \Delta AOC = \Delta AOB\left( {c.c.c} \right)\), suy ra: \(\widehat {HOB} = \widehat {HOG} = \widehat {GOF} = \widehat {EOF} = \widehat {DOE} = \widehat {COD} = \widehat {AOC} = \widehat {AOB} = \frac{{{{360}^o}}}{8} = {45^o}\)

+ Tính góc AOG

+ Để cabin A di chuyển đến vị trí cao nhất (vị trí cabin G) thì vòng quay phải quay theo chiều thuận kim đồng hồ quanh tâm góc \({135^o}\).

Lời giải chi tiết

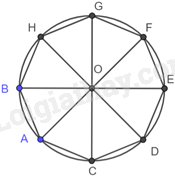
Gọi tám cabin tạo thành một bát giác đều BACDEFGH nội tiếp đường tròn (O).

Vì BACDEFGH là bát giác đều nên

\(AB = AC = CD = DE = EF = FG = GH = HB\)

Vì BACDEFGH là bát giác nội tiếp đường tròn (O) nên

\(OA = OB = OC = OD = OE = OF = OH = OG\)

Do đó

\(\Delta HOB = \Delta HOG = \Delta FOG = \Delta FOE = \Delta DOE = \Delta DOC = \Delta AOC = \Delta AOB\left( {c.c.c} \right)\)

Suy ra

\(\widehat {HOB} = \widehat {HOG} = \widehat {GOF} = \widehat {EOF} = \widehat {DOE} = \widehat {COD} = \widehat {AOC} = \widehat {AOB} = \frac{{{{360}^o}}}{8} = {45^o}\)

Ta có:

\(\widehat {AOG} = \widehat {AOB} + \widehat {BOH} + \widehat {HOG} = {45^o} + {45^o} + {45^o} = {135^o}\)

Để cabin A di chuyển đến vị trí cao nhất (vị trí cabin G) thì vòng quay phải quay theo chiều thuận kim đồng hồ quanh tâm góc \({135^o}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 9.29 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức
Liệt kê năm phép quay giữ nguyên một ngũ giác đều nội tiếp một đường tròn tâm O.
Giải bài tập 9.28 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức
Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.54. Phép quay ngược chiều ({60^o}) tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.
Giải bài tập 9.27 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức
Cho hình thoi ABCD có (widehat A = {60^o}). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Giải bài tập 9.26 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức
Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2cm. Tính độ dài các cạnh của tam giác ABC.
Giải bài tập 9.25 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức
Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều ({60^o}) tâm O biến điểm M thành điểm N?
Giải bài tập 9.24 trang 89 SGK Toán 9 tập 2 - Kết nối tri thức
Trong các hình phẳng sau (H.9.52), hình nào là hình phẳng có dạng đa giác đều?
Giải mục 2 trang 87, 88, 89 SGK Toán 9 tập 2 - Kết nối tri thức
Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B. Em hãy so sánh khoảng cách từ hai điểm A và B đến điểm O. Hai điểm A, B có cùng nằm trên một đường tròn tâm O hay không?
Giải mục 1 trang 84, 85, 86 SGK Toán 9 tập 2 - Kết nối tri thức
Ta đã biết các tam giác đều và hình vuông có các đỉnh nằm trên một đường tròn. Ta dựng một đa giác lồi 5 cạnh có các đỉnh nằm trên một đường tròn như sau: - Vẽ đường tròn tâm O bán kính R. - Lần lượt lấy các điểm A, B, C, D, E trên đường tròn theo thứ tự ngược chiều kim đồng hồ (hoặc theo chiều kim đồng hồ) sao cho: (widehat {AOB} = widehat {BOC} = widehat {COD} = widehat {DOE} = widehat {EOA} = frac{{{{360}^o}}}{5} = {72^o}). Em hãy giải thích vì sao các cạnh và các góc của đa giác
Lý thuyết Đa giác đều Toán 9 Kết nối tri thức
1. Đa giác đều Đa giác Những hình như dưới đây được gọi chung là các đa giác.