Giải bài tập 8 trang 80 sách bài tập toán 12 - Chân trời sáng tạo

Một công ty bảo hiểm ô tô nhận thấy nếu một tài xế gặp sự cố trong một năm thì xác suất gặp sự cố ở năm tiếp theo là 0,2; còn nếu trong một năm không gặp sự cố nào thì xác suất gặp sự cố ở năm tiếp theo là 0,05. Xác suất để một tài xế gặp sự cố ở năm đầu tiên lái xe là 0,1. Sử dụng sơ đồ hình cây: a) Tính xác suất để một tài xế không gặp sự cố nào trong 2 năm đầu tiên lái xe. b) Tính xác suất để một tài xế gặp sự cố trong cả 2 năm đầu tiên lái xe. Làm tròn kết quả đến hàng phần trăm.

Đề bài

Một công ty bảo hiểm ô tô nhận thấy nếu một tài xế gặp sự cố trong một năm thì xác suất gặp sự cố ở năm tiếp theo là 0,2; còn nếu trong một năm không gặp sự cố nào thì xác suất gặp sự cố ở năm tiếp theo là 0,05. Xác suất để một tài xế gặp sự cố ở năm đầu tiên lái xe là 0,1. Sử dụng sơ đồ hình cây:

a) Tính xác suất để một tài xế không gặp sự cố nào trong 2 năm đầu tiên lái xe.

b) Tính xác suất để một tài xế gặp sự cố trong cả 2 năm đầu tiên lái xe. Làm tròn kết quả đến hàng phần trăm.

Phương pháp giải - Xem chi tiết

Sử dụng sơ đồ hình cây.

Lời giải chi tiết

Gọi \(A\) là biến cố “Tài xế không gặp sự cố trong năm đầu tiên lái xe”, \(B\) là biến cố “Tài xế không gặp sự cố trong năm thứ hai lái xe”.

Xác suất để một tài xế gặp sự cố ở năm đầu tiên lái xe là 0,1 nên ta có \(P\left( {\overline A } \right) = 0,1\).

Do đó \(P\left( A \right) = 1 - P\left( {\overline A } \right) = 1 - 0,1 = 0,9\).

Nếu một tài xế gặp sự cố trong một năm thì xác suất gặp sự cố ở năm tiếp theo là 0,2 nên ta có \(P\left( {\overline B |\overline A } \right) = 0,2\).

Do đó \(P\left( {B|\overline A } \right) = 1 - P\left( {\overline B |\overline A } \right) = 1 - 0,2 = 0,8\).

Nếu trong một năm không gặp sự cố nào thì xác suất gặp sự cố ở năm tiếp theo là 0,05 nên ta có \(P\left( {\overline B |A} \right) = 0,05\).

Do đó \(P\left( {B|A} \right) = 1 - P\left( {\overline B |A} \right) = 1 - 0,05 = 0,95\).

Ta có sơ đồ hình cây như sau:

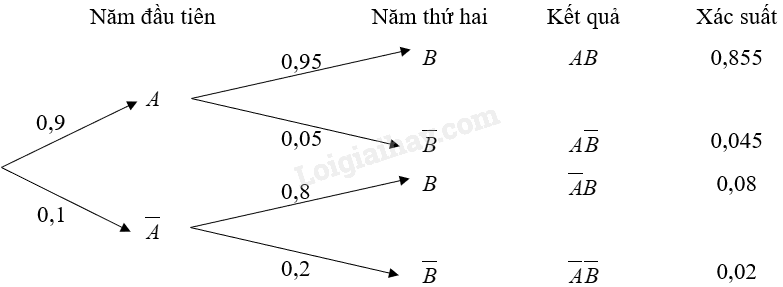
a) Xác suất để một tài xế không gặp sự cố nào trong 2 năm đầu tiên lái xe là: \(P\left( {AB} \right) = 0,855\).

b) Xác suất để một tài xế gặp sự cố trong cả 2 năm đầu tiên lái xe là \(P\left( {\overline A \overline B } \right) = 0,02\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 9 trang 80 sách bài tập toán 12 - Chân trời sáng tạo
Trong một đợt khám sức khoẻ, người ta thấy có 15% người dân ở một khu vực mắc bệnh béo phì. Tỉ lệ người béo phì và thường xuyên tập thể dục là 2%. Biết rằng tỉ lệ người thường xuyên tập thể dục ở khu vực đó là 40%. Theo kết quả điều tra trên, việc tập thể dục sẽ làm giảm khả năng bị béo phì đi bao nhiêu lần?
Giải bài tập 10 trang 80 sách bài tập toán 12 - Chân trời sáng tạo
Các sản phẩm của một phân xưởng được đóng thành hộp, mỗi hộp gồm 10 sản phẩm. Các hộp sản phẩm được kiểm tra như sau: người ta lấy ra ngẫu nhiên 1 sản phẩm từ hộp, nếu sản phẩm đó xấu, hộp sẽ bị loại; nếu sản phẩm đó tốt, người ta sẽ chọn ngẫu nhiên thêm 1 sản phẩm khác từ hộp để kiểm tra. Hộp sẽ chỉ được chấp nhận nếu không có sản phẩm xấu nào trong các sản phẩm được chọn kiểm tra. Biết có một hộp chứa 2 sản phẩm xấu. Tính xác suất để hộp đó không được chấp nhận. Làm tròn kết quả đến hàng phầ
Giải bài tập 7 trang 80 sách bài tập toán 12 - Chân trời sáng tạo
Cho hai biến cố \(A\) và \(B\) thoả mãn \(P\left( A \right) = P\left( B \right) = 0,8\). Chứng minh rằng \(P\left( {A|B} \right) \ge 0,75\).
Giải bài tập 6 trang 80 sách bài tập toán 12 - Chân trời sáng tạo
Cho hai biến cố độc lập (A) và (B) có (Pleft( A right) = 0,4;Pleft( B right) = 0,8). Tính (Pleft( {A|A cup B} right)). Làm tròn kết quả đến hàng phần trăm.
Giải bài tập 5 trang 80 sách bài tập toán 12 - Chân trời sáng tạo
Cho hai biến cố (A,B) có (Pleft( {overline A B} right) = 0,2;Pleft( {AB} right) = 0,3) và (Pleft( {Aoverline B } right) = 0,4). Tính (Pleft( {A|B} right);Pleft( {A|overline B } right);Pleft( {overline A |B} right);Pleft( {overline A |overline B } right)).
Giải bài tập 4 trang 80 sách bài tập toán 12 - Chân trời sáng tạo
Cho hai biến cố \(A,B\) có \(P\left( A \right) = 0,4;P\left( B \right) = 0,8;P\left( {A \cup B} \right) = 0,9\). Tính \(P\left( {A|B} \right);P\left( {A|\overline B } \right);P\left( {\overline A |B} \right);P\left( {\overline A |\overline B } \right)\).
Giải bài tập 3 trang 80 sách bài tập toán 12 - Chân trời sáng tạo
Cho hai biến cố \(A,B\) có \(P\left( A \right) = 0,7;P\left( B \right) = 0,3;P\left( {A|B} \right) = 0,6\). Tính \(P\left( {B|A} \right)\). Làm tròn kết quả đến hàng phần trăm.
Giải bài 2 trang 79 sách bài tập toán 12 - Chân trời sáng tạo
Một lớp học có 40% học sinh là nam. Số học sinh nữ bị cận thị chiếm 20% số học sinh trong lớp. Chọn ngẫu nhiên 1 học sinh của lớp. Tính xác suất học sinh đó bị cận thị, biết rằng đó là học sinh nữ. Làm tròn kết quả đến hàng phần trăm.
Giải bài tập 1 trang 79 sách bài tập toán 12 - Chân trời sáng tạo
Một hợp chứa 15 tấm thẻ cùng loại được ghi số từ 1 đến 15. Các thẻ có số từ 1 đến 10 được sơn màu đỏ, các thể còn lại được sơn màu xanh. Bạn Việt chọn ra ngẫu nhiên 1 thẻ từ hộp. a) Tính xác suất để thẻ được chọn có màu đỏ, biết rằng nó được ghi số chẵn. Làm tròn kết quả đến hàng phần trăm. b) Tính xác suất để thể được chọn ghi số chẵn, biết rằng nó có màu xanh.