Giải bài tập 5.31 trang 126 SGK Toán 9 tập 1 - Cùng khám phá

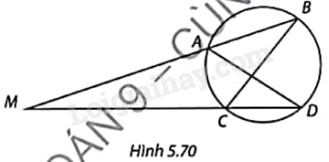
Trong Hình 5.70, hai cát tuyến AB và CD của đường tròn cắt nhau tại M. a) Chứng minh rằng $\Delta AMD\backsim \Delta CMB$. b) Tính MB và MC, biết $MD = 100,MA = 70,AD = 40,BC = 42$.

Đề bài

Trong Hình 5.70, hai cát tuyến AB và CD của đường tròn cắt nhau tại M.

a) Chứng minh rằng $\Delta AMD\backsim \Delta CMB$.

b) Tính MB và MC, biết $MD = 100,MA = 70,AD = 40,BC = 42$.

Phương pháp giải - Xem chi tiết

a) + Vì góc MDA và góc MBC là góc nội tiếp cùng chắn cung AC nên $\widehat {MDA} = \widehat {MBC}$.

+ Chứng minh $\Delta AMD\backsim \Delta CMB\left( g.g \right)$.

b) + Vì $\Delta AMD\backsim \Delta CMB$ nên $\frac{{MA}}{{MC}} = \frac{{MD}}{{MB}} = \frac{{AD}}{{CB}}$, suy ra $\frac{{70}}{{MC}} = \frac{{100}}{{MB}} = \frac{{40}}{{42}} = \frac{{20}}{{21}}$, từ đó tính MC, MB.

Lời giải chi tiết

a) Vì góc MDA và góc MBC là góc nội tiếp cùng chắn cung AC nên $\widehat {MDA} = \widehat {MBC}$.

Tam giác AMD và tam giác CMB có:

$\widehat {MDA} = \widehat {MBC}$,

góc M chung.

Do đó, $\Delta AMD\backsim \Delta CMB\left( g.g \right)$.

b) Vì $\Delta AMD\backsim \Delta CMB$ nên $\frac{{MA}}{{MC}} = \frac{{MD}}{{MB}} = \frac{{AD}}{{CB}}$, suy ra $\frac{{70}}{{MC}} = \frac{{100}}{{MB}} = \frac{{40}}{{42}} = \frac{{20}}{{21}}$.

Do đó, $MC = 70:\frac{{20}}{{21}} = \frac{{147}}{2}$, $MB = 100:\frac{{20}}{{21}} = 105$.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 5.32 trang 126 SGK Toán 9 tập 1 - Cùng khám phá
Trên vòng đu quay tâm O, hai bạn An và Bình ngồi ở hai cabin tại điểm A và B kế tiếp nhau, bạn Cường ngồi trên cabin tại điểm C như Hình 5.71. Từ vị trí của mình, bạn Cường đo được $\widehat {ACB} = 7,{5^o}$. Tính số đo cung AB, từ đó tính số cabin của vòng đu quay.
Giải bài tập 5.30 trang 126 SGK Toán 9 tập 1 - Cùng khám phá
Tính các số đo x và y trong mỗi trường hợp ở Hình 5.69.
Giải mục 2 trang 124, 125 SGK Toán 9 tập 1 - Cùng khám phá
Trong Hình 5.63, $\widehat {AOB} = {70^o}$. a) Sử dụng thước đo góc, xác định số đo các góc nội tiếp AMB, ANB, APB chắn cung AB. b) Nhận xét về mối liên hệ giữa số đo các góc nội tiếp trên với số đo cung nhỏ AB.
Giải mục 1 trang 123 SGK Toán 9 tập 1 - Cùng khám phá
Quan sát hình ngôi sao năm cánh trong Hình 5.60, đỉnh và cạnh của góc CAD có liên hệ như thế nào với đường tròn khung của lồng đèn ông sao?
Giải câu hỏi khởi động trang 123 SGK Toán 9 tập 1 - Cùng khám phá
Góc ở đỉnh của mỗi cánh của lồng đèn ông sao trong Hình 5.60 có số đo bằng bao nhiêu?
Lý thuyết Góc nội tiếp Toán 9 Cùng khám phá
1. Góc nội tiếp Định nghĩa Góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây của đường tròn được gọi là một góc nội tiếp của đường tròn.