Giải bài tập 5.19 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức

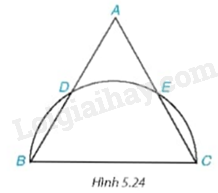
Cho tam giác đều ABC có AB = ({rm{2}}sqrt 3 )cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24). a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy. b) Tính diện tích của hình viên phân (xem ví dụ 2) giới hạn bởi dây BD và cung nhỏ BD.

Đề bài

Cho tam giác đều ABC có AB = \({\rm{2}}\sqrt 3 \)cm. Nửa đường tròn đường kính BC cắt hai cạnh AB và AC lần lượt tại D và E (khác B và C) (H.5.24).

a) Chứng tỏ rằng ba cung nhỏ BD, DE và EC bằng nhau. Tính số đo mỗi cung ấy.

b) Tính diện tích của hình viên phân (xem ví dụ 2) giới hạn bởi dây BD và cung nhỏ BD.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Chứng mình tam giác OBD đều, từ đó suy ra \(\widehat {{\rm{BOD}}} = 60^\circ \). Tương tự có: \(\widehat {{\rm{BOD}}} = \widehat {{\rm{COE}}} = \widehat {{\rm{DOE}}} = 60^\circ \) hay số đo các cung nhỏ BD, DE và EC bằng nhau.

b) Áp dụng công thức tính diện tích hình viên phân: \(S = {R^2}\left( {\frac{\pi }{4} - \frac{1}{2}} \right)\)

Lời giải chi tiết

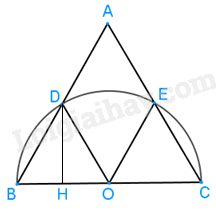
a) Gọi O là trung điểm của BC

Vì OB = OD nên tam giác OBD là tam giác cân tại O

Mà \(\widehat {{\rm{OBD}}} = 60^\circ \)(do tam giác ABC đều)

Suy ra tam giác OBD đều.

Do đó: \(\widehat {{\rm{BOD}}} = 60^\circ \)

Tương tự ta có: \(\widehat {{\rm{COE}}} = 60^\circ \)

Lại có: \(\widehat {{\rm{BOD}}} + \widehat {{\rm{DOE}}} + \widehat {{\rm{COE}}} = 180^\circ \Rightarrow \widehat {{\rm{DOE}}} = 60^\circ \)

Khi đó: \(\widehat {{\rm{BOD}}} = \widehat {{\rm{COE}}} = \widehat {{\rm{DOE}}} = 60^\circ \)

Hay sđ\(\overset\frown{BD}=\) sđ\(\overset\frown{CE}=\) sđ\(\overset\frown{DE}=60{}^\circ \)

b) Đường tròn (O) có bán kính \(OA = \frac{{AB}}{2} = \frac{{{\rm{2}}\sqrt 3 }}{2} = \sqrt 3 \)(cm)

\(S_q = \frac{60}{360}.\pi.(\sqrt{3})^2 = \frac{\pi}{2} (cm^2) \)

Kẻ \(DH \bot OB\), tam giác OBD đều nên DH cũng là đường trung tuyến, suy ra H là trung điểm của OB.

Suy ra \( OH = \frac{OB}{2} = \frac{\sqrt 3}{2}\)

Áp dụng định lí Pythagore vào tam giác ODH, ta có:

\(DH = \sqrt{OD^2-OH^2} = \sqrt{3 - \left({\frac{\sqrt3}{2}}\right)^2} = \frac{3}{2}\)

Diện tích tam giác OBD là:

\(S_{\Delta OBD} = \frac{DH.OB}{2} = \frac{3.\sqrt3}{2.2} = \frac{3\sqrt3}{4}\)

Diện tích hình viên phân là:

\(S_{vp} = S_q - S_{\Delta OBD} = \frac{\pi}{2} - \frac{3\sqrt3}{4} \approx 0,27 (cm^2)\)

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 4 phiếu

Bài tiếp theo

Giải bài tập 5.18 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức
Ba bộ phận truyền chuyển động của một chiếc xe đạp gồm một giò đĩa (bánh răng gắn với bàn đạp), một chiếc líp (cũng có dạng bánh răng) gắn với bánh xe và bộ xích (H.5.23). Biết rằng giò đĩa có bán kính 15 cm, líp có bán kính 4 cm và bánh xe có đường kính 65 cm. Hỏi khi người đi xe đạp một vòng thì xe chạy được quãng đường dài bao nhiêu mét (làm tròn kết quả đến hàng phần chục)?
Giải bài tập 5.17 trang 98 SGK Toán 9 tập 1 - Kết nối tri thức
Cho đường tròn (O; 5 cm). a) Hãy nêu cách vẽ dây AB sao cho khoảng cách từ điểm O đến dây AB bằng 2,5 cm. b) Tính độ dài của dây AB trong câu a (làm tròn đến hàng phần trăm). c) Tính số đo và độ dài của cung nhỏ AB. d) Tính diện tích hình quạt tròn ứng với cung nhỏ AB.
Giải bài tập 5.16 trang 97 SGK Toán 9 tập 1 - Kết nối tri thức
Có thể xem guồng nước (còn gọi là cọn nước) là một công cụ hay cỗ máy có dạng hình tròn, quay được nhờ sức nước chảy (H.5.22a). Guồng nước thường thấy ở các vùng miền núi. Nhiều guồng nước được làm bằng tre, dùng để đưa nước lên ruộng cao, giã gạo hoặc làm một số việc khác. Giả sử ngấn nước ngăn cách giữa phần trên và phần dưới của một guồng nước được biểu thị bởi cung ứng với một dây dài 4 m và điểm ngập sâu nhất là 0,5 m (trên hình 5.22b, điểm ngập sâu nhất là điểm C, ta có AB = 4 m và HC = 0
Giải bài tập 5.15 trang 97 SGK Toán 9 tập 1 - Kết nối tri thức
Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng: a) Đường tròn đường kính BC đi qua các điểm H và K; b) KH < BC.
Giải bài tập 5.14 trang 97 SGK Toán 9 tập 1 - Kết nối tri thức
Cho dây AB không qua tâm của đường tròn (O) . Gọi A’ và B’ là hai điểm lần lượt đối xứng với A và B qua (O) . Hỏi đường trung trực của A’B’ có phải là trục đối xứng của (O) hay không? Tại sao?