Giải bài tập 5 trang 14 SGK Toán 12 tập 1 - Cánh diều

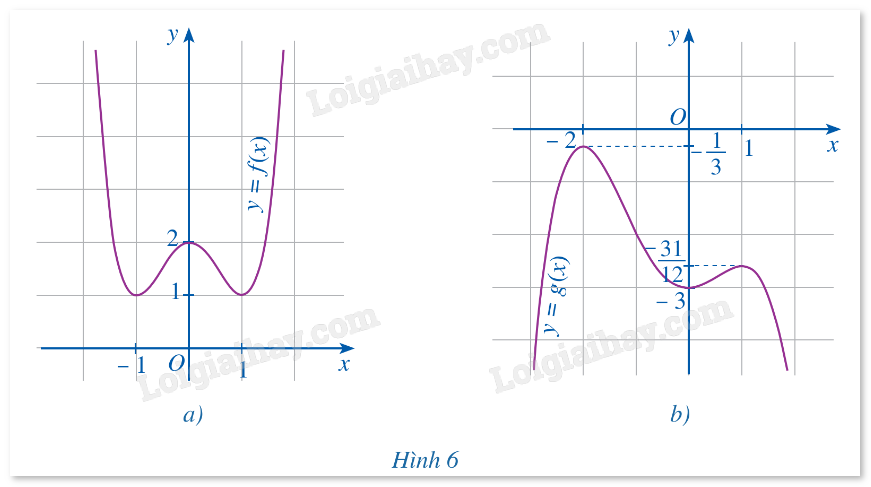
Cho hai hàm số (y = fleft( x right),y = gleft( x right)) có đồ thị hàm số lần lượt ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.

Đề bài

Cho hai hàm số \(y = f(x) = {x^4} - 2{x^2} + 2,\) \(y = - \frac{1}{4}{x^4} - \frac{1}{3}{x^3} + {x^2} - 3\) có đồ thị lần lượt được cho ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực tiểu của mỗi hàm số đó.

Phương pháp giải - Xem chi tiết

Dựa vào đồ thị hàm số và nhận xét

Lời giải chi tiết

a) Hàm số đồng biến trên khoảng \(( - 1;0)\) và \((1; + \infty )\), nghịch biến trên khoảng \(( - \infty ; - 1)\) và \((0;1)\). Hàm số đạt cực tiểu tại \(x = - 1\) và \(x = 1\), đạt cực đại tại \(x = 0\).

b) Hàm số đồng biến trên khoảng \(( - \infty ; - 2)\) và \((0;1)\), nghịch biến trên khoảng \(( - 2;0)\) và \((1; + \infty )\). Hàm số đạt cực tiểu tại \(x = 0\), đạt cực đại tại \(x = - 2\) và \(x = 1\).

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 6 trang 14 SGK Toán 12 tập 1 - Cánh diều
Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) được tính bởi công thức sau: \(V\left( T \right) = 999,87 - 0,06426T + 0,0085043{T^2} - 0,0000679{T^3}\). Hỏi thể tích \(V\left( T \right)\),\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) giảm trong khoảng nhiệt độ nào?
Giải bài tập 7 trang 14 SGK Toán 12 tập 1 - Cánh diều
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm (t = 0left( s right)) cho đến khi tên lửa đẩy được phóng đi tại thời điểm (t = 126left( s right)), cho bởi hàm số sau: (vleft( t right) = 0,001320{t^3} - 0,09029{t^2} + 23). (v được tính bằng ft/s, 1 feet = 0,3048 m) Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đế
Giải bài tập 4 trang 13 SGK Toán 12 tập 1 - Cánh diều
Tìm cực trị của mỗi hàm số sau: a) (y = 2{x^3} + 3{x^2} - 36x - 10) b) (y = -{x^4} - 2{x^2} - 3) c) (y = x + frac{1}{x})
Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Cánh diều
Tìm các khoảng đơn điệu của hàm số sau: a) \(y = - {x^3} + 2{x^2} - 3\) b) \(y = {x^4} + 2{x^2} + 5\) c) \(y = \frac{{3x + 1}}{{2 - x}}\) d) \(y = \frac{{{x^2} - 2x}}{{x + 1}}\)
Giải bài tập 2 trang 13 SGK Toán 12 tập 1 - Cánh diều
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau: Giá trị cực tiểu của hàm số đã cho bằng: a) \(2\). b) \(3\). c) \( - 4\). d) \(0\).
Giải bài tập 1 trang 13 SGK Toán 12 tập 1 - Cánh diều
Cho hàm số \(y = f\left( x \right)\)có bảng biến thiên như sau: Hàm số đồng biến trên khoảng nào dưới đây? A. \(\left( {1; + \infty } \right)\). B. \(\left( { - 1;0} \right)\). C. \(\left( { - 1;1} \right)\). D. \(\left( {0;1} \right)\).
Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Cánh diều
Điểm cực trị, giá trị cực trị của hàm số
Giải mục 1 trang 5, 6, 7 SGK Toán 12 tập 1 - Cánh diều
Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
Lý thuyết Tính đơn điệu của hàm số Toán 12 Cánh Diều
1.Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm