Giải bài tập 7 trang 13 SGK Toán 12 tập 1 - Cánh diều
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm (t = 0left( s right)) cho đến khi tên lửa đẩy được phóng đi tại thời điểm (t = 126left( s right)), cho bởi hàm số sau: (vleft( t right) = 0,001320{t^3} - 0,09029{t^2} + 23). (v được tính bằng ft/s, 1 feet = 0,3048 m) Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đế
Đề bài
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm \(t = 0\left( s \right)\) cho đến khi tên lửa đẩy được phóng đi tại thời điểm \(t = 126\left( s \right)\), cho bởi hàm số sau:
\(v\left( t \right) = 0,001302{t^3} - 0,09029{t^2} + 23\).
(v được tính bằng ft/s, 1 feet = 0,3048 m)
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Phương pháp giải - Xem chi tiết
B1: Tìm tập xác định của hàm số.
B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.
B3: Lập bảng biến thiên.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết
Tập xác định: \(D = \mathbb{R}\).
Ta có: \(a\left(t\right)=v'\left( t \right) = 3 \times 0,001302{t^2} - 2 \times 0,09029t\)
\(a'(t) = 7,{812.10^{ - 3}}t - 0,18058\)
Nhận xét \(a'\left( t \right) = 0 \Leftrightarrow t \approx 23,1\).
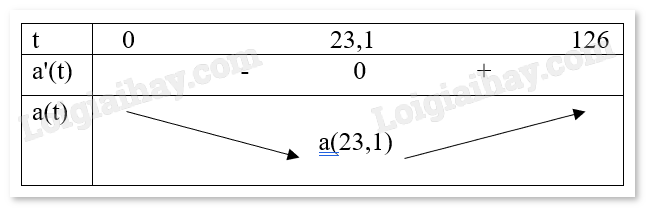
Vậy gia tốc tàu con thoi tăng từ giây thứ \(23,1\) đến giây thứ 126.
Các bài khác cùng chuyên mục













Danh sách bình luận