Giải mục 1 trang 5, 6, 7 SGK Toán 12 tập 1 - Cánh diều
Nhận biết tính đơn điệu của hàm số bằng dấu của đạo hàm
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 5 SGK Toán 12 Cánh diều
a) Nêu định nghĩa hàm số đồng biến, hàm số nghịch biến trên tập \(K \subset \mathbb{R}\), trong đó K là một khoảng, đoạn hoặc nửa khoảng.
b) Cho hàm số \(y = f\left( x \right) = {x^2}\) có đồ thị như Hình 2.
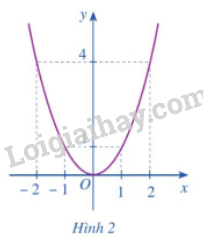
- Xác định khoảng đồng biến, khoảng nghịch biến của hàm số đó.
- Xét dấu đạo hàm \(f'\left( x \right) = 2x\).
- Nêu mối liên hệ giữa sự đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2}\) và dấu của đạo hàm \(f'\left( x \right) = 2x\) trên mỗi khoảng \(\left( { - \infty ;0} \right),\left( {0; + \infty } \right)\).
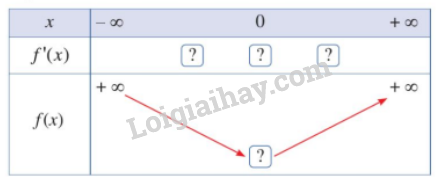
- Hoàn thành bảng biến thiên sau:
Phương pháp giải:
Dựa vào định nghĩa hàm số đồng biến, nghịch biến trên tập K.
Lời giải chi tiết:
a) Cho K là một khoảng, một đoạn hoặc một nửa khoảng và \(f\left( x \right)\) là hàm số xác định trên K.
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).
- Hàm số \(f\left( x \right)\) được gọi là hàm số đồng biến trên K nếu với mọi \({x_1},{x_2}\) thuộc K và \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).
- Hàm số đồng biến hoặc nghịch biến trên K còn được gọi là hàm số đơn điệu trên K.
b)
- Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
- Đạo hàm \(f'\left( x \right) = 2x\)âm khi \(x < 0\) và dương khi \(x > 0\).
- Hàm số \(y = f\left( x \right) = {x^2}\) nghịch biến khi \(f'\left( x \right) = 2x\)mang dấu âm và đồng biến khi \(f'\left( x \right) = 2x\) mang dấu dương.
- Ta có bàng biến thiên sau:
LT1
Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Cánh diều
Xét dấu \(y'\) rồi tìm khoảng đồng biến, nghịch biến của hàm số\(y = \frac{4}{3}{x^3} - 2{x^2} + x - 1\).
Phương pháp giải:
B1: Tính \(y'\)rồi lập bảng xét dấu của \(y'\).
B2. Dựa vào bảng xét dấu của \(y'\) để nhận xét khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^2} - 4x + 1\).
Xét \(y' = 0 \Leftrightarrow x = \frac{1}{2}\).

Vậy hàm số đồng biến trên \(\mathbb{R}\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 6 SGK Toán 12 Cánh diều
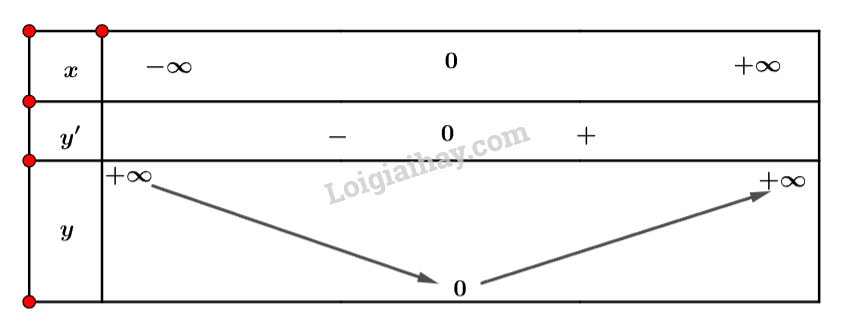
Tìm các khoảng đơn điệu của hàm số \(y = {x^4} + 2{x^2} - 3\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 4{x^3} + 4x\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:

Vậy hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 7 SGK Toán 12 Cánh diều
a) Xác định tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^3}\).
b) Xét dấu của đạo hàm \(f'\left( x \right) = 3{x^2}\).
c) Phương trình \(f'\left( x \right) = 0\) có bao nhiêu nghiệm?
Phương pháp giải:
Dựa vào định nghĩa đồng biến, nghịch biến của hàm số và các bước xét tính đồng biến, nghịch biến của hàm số.
Lời giải chi tiết:
a) Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = 3{x^2}\).
Xét \(y' = 0 \Rightarrow x = 0\).
Bảng biến thiên:
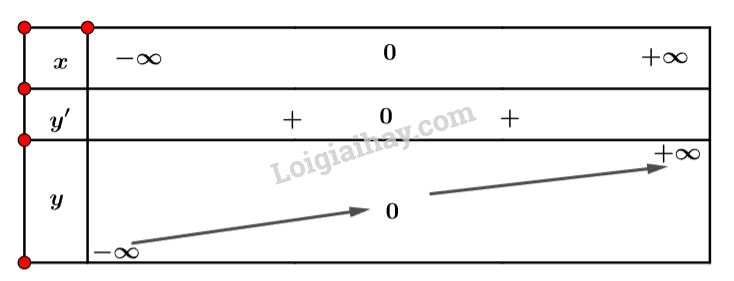
Vậy hàm số đồng biến trên \(\mathbb{R}\).
b) Dựa vào bảng biến thiên ta thấy đạo hàm \(y' = 3{x^2}\) luôn dương với mọi x.
c) Phương trình \(f'\left( x \right) = 0\) có một nghiệm.
LT3
Trả lời câu hỏi Luyện tập 3 trang 7 SGK Toán 12 Cánh diều
Chứng minh rằng hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\).
Ta có: \(y' = \frac{x}{{\sqrt {{x^2} + 1} }}\).
Xét \(y' = 0 \Leftrightarrow x = 0\).
Ta có bảng biến thiên:

Vậy hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( - \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).
LT4
Trả lời câu hỏi Luyện tập 4 trang 8 SGK Toán 12 Cánh diều
Tìm các khoảng đơn điệu của hàm số sau \(y = \frac{{2x - 1}}{{x + 2}}\).
Phương pháp giải:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y'\). Tìm các điểm mà tại đó \(y' = 0\) hoặc \(y'\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải chi tiết:
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{5}{{{{\left( {x + 2} \right)}^2}}}\).
Nhận xét: \(y' > 0\) với mọi \(x \in D\).
Ta có bảng biến thiên:

Vậy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( { - 2; + \infty } \right)\).
Các bài khác cùng chuyên mục













Danh sách bình luận