-
Toán 9 tập 1 - Cánh diều
-
Toán 9 tập 2 - Cánh diều
Giải bài tập 5 trang 110 SGK Toán 9 tập 1 - Cánh diều
Cho đường tròn (left( {O;R} right)) đường kính (AB) và các đường thẳng (m,n,p) lần lượt tiếp xúc với đường tròn tại (A,B,C) (Hình 43). Chứng minh: a) (AD + BE = DE); b) (widehat {COD} = frac{1}{2}widehat {COA}) và (widehat {COE} = frac{1}{2}widehat {COB}); c) Tam giác (ODE) vuông; d) (frac{{OD.OE}}{{DE}} = R).
Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - KHTN - Lịch sử và Địa lí
Đề bài
Cho đường tròn \(\left( {O;R} \right)\) đường kính \(AB\) và các đường thẳng \(m,n,p\) lần lượt tiếp xúc với đường tròn tại \(A,B,C\) (Hình 43).
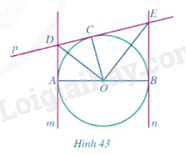
Chứng minh:
a) \(AD + BE = DE\);
b) \(\widehat {COD} = \frac{1}{2}\widehat {COA}\) và \(\widehat {COE} = \frac{1}{2}\widehat {COB}\);
c) Tam giác \(ODE\) vuông;
d) \(\frac{{OD.OE}}{{DE}} = R\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dựa vào tính chất tiếp tuyến để chứng minh.
Lời giải chi tiết
a) Do \(DC,DA\) cùng là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(DA = DC\).
Do \(EC,EB\) cùng là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(CE = BE\).
Lại có: \(DC + CE = DE\) suy ra \(DA + EB = DE\).
b) Do \(DC,DA\) cùng là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(OD\) là tia phân giác của góc \(COA\).
Suy ra \(\widehat {COD} = \frac{1}{2}\widehat {COA}\).
Do \(EC,EB\) cùng là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(OE\) là tia phân giác của góc \(COB\).
Suy ra \(\widehat {COE} = \frac{1}{2}\widehat {COB}\).
c) Ta có: \(\widehat {COA} + \widehat {COB} = 180^\circ \) (hai góc kề bù).
Suy ra \(\frac{1}{2}\left( {\widehat {COA} + \widehat {COB}} \right) = \frac{1}{2}.180^\circ = 90^\circ\)
Do đó \(\frac{1}{2}\widehat {COA} + \frac{1}{2}\widehat {COB} = 90^\circ .\)
Mà \(\widehat {COD} = \frac{1}{2}\widehat {COA}\),\(\widehat {COE} = \frac{1}{2}\widehat {COB}\) nên \(\widehat {COD} + \widehat {COE} = 90^\circ \) hay \(\widehat {DOE} = 90^\circ \).
Vậy tam giác \(ODE\) vuông tại \(O\).
d) Vì \(DE\) là tiếp tuyến của \((O)\) nên \(DE \perp CO\)
Suy ra \( \widehat{DCO} = 90^\circ\)
Xét \(\Delta ODE\) và \(\Delta CDO\) có:
\(\widehat{DOE} = \widehat{DCO} = 90^\circ\)
\(\widehat{ODE}\) (góc chung)
suy ra \(\Delta ODE \backsim \Delta CDO\) (g.g)
Do đó \( \frac{OE}{OC} = \frac{DE}{OD}\)
Dẫn đến \(OE \cdot OD = DE \cdot OC\)
Suy ra \(\frac{{OD.OE}}{{DE}} = OC\).
hay \(\frac{{OD.OE}}{{DE}} = R\). (đpcm)
Bình luận
Chia sẻ
- Giải bài tập 4 trang 110 SGK Toán 9 tập 1 - Cánh diều
- Giải bài tập 3 trang 110 SGK Toán 9 tập 1 - Cánh diều
- Giải bài tập 2 trang 110 SGK Toán 9 tập 1 - Cánh diều
- Giải bài tập 1 trang 109 SGK Toán 9 tập 1 - Cánh diều
- Giải mục 2 trang 108, 109 SGK Toán 9 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
