Giải bài tập 3 trang 110 SGK Toán 9 tập 1 - Cánh diều

Cho đường tròn (left( O right)) và điểm (M) nằm ngoài đường tròn. Hai đường thẳng thẳng (c,d) đi qua (M) lần lượt tiếp xúc với (left( O right)) tại (A,B). Tia phân giác của góc (MAB) cắt (MO) tại (I). Chứng minh điểm (I) cách đều ba đường thẳng (MA,MB) và (AB).

Tổng hợp đề thi giữa kì 1 lớp 9 tất cả các môn - Cánh diều

Toán - Văn - Anh - Khoa học tự nhiên

Đề bài

Cho đường tròn \(\left( O \right)\) và điểm \(M\) nằm ngoài đường tròn. Hai đường thẳng thẳng \(c,d\) đi qua \(M\) lần lượt tiếp xúc với \(\left( O \right)\) tại \(A,B\). Tia phân giác của góc \(MAB\) cắt \(MO\) tại \(I\). Chứng minh điểm \(I\) cách đều ba đường thẳng \(MA,MB\) và \(AB\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựa vào tính chất tiếp tuyến để chứng minh.

Lời giải chi tiết

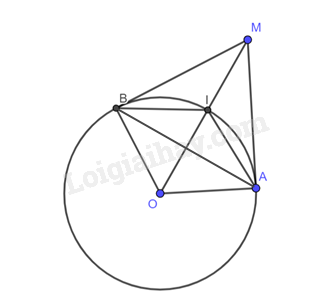
Do \(MA,MB\) là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(MO\) là tia phân giác của \(\widehat {AMB}\) hay \(MI\) là tia phân giác của \(\widehat {AMB}\).

Xét tam giác \(AMB\) có:

\(BI\) là tia phân giác của góc \(MAB\);

\(MI\) là tia phân giác của góc \(AMB\).

Suy ra \(I\) là giao điểm của 3 đường phân giác tam giác \(AMB\).

Vậy \(I\) cách đều \(MA,MB,AB\).

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 6 phiếu

Bài tiếp theo

Giải bài tập 4 trang 110 SGK Toán 9 tập 1 - Cánh diều
Một người quan sát đặt mắt ở vị trí (A) có độ cao cách mực nước biển là (AB = 5m). Cắt bề mặt Trái Đất bởi một mặt phẳng đi qua điểm (A) và tâm của Trái Đất thì phần chung giữa chúng là một đường tròn lớn tâm (O) như Hình 42. Tầm quan sát tối đa từ vị trí (A) là đoạn (AC), trong đó (C) là tiếp điểm của tiếp tuyến đi qua (A) với đường tròn (left( O right)). Tính độ dài đoạn thẳng (AC) (theo đơn vị kilômét và làm tròn kết quả đến hàng phần mười), biết bán kính Trái Đất là: (
Giải bài tập 5 trang 110 SGK Toán 9 tập 1 - Cánh diều
Cho đường tròn (left( {O;R} right)) đường kính (AB) và các đường thẳng (m,n,p) lần lượt tiếp xúc với đường tròn tại (A,B,C) (Hình 43). Chứng minh: a) (AD + BE = DE); b) (widehat {COD} = frac{1}{2}widehat {COA}) và (widehat {COE} = frac{1}{2}widehat {COB}); c) Tam giác (ODE) vuông; d) (frac{{OD.OE}}{{DE}} = R).
Giải bài tập 2 trang 110 SGK Toán 9 tập 1 - Cánh diều
Cho đường tròn (left( O right)) và dây (AB). Điểm (M) nằm ngoài đường tròn (left( O right)) thỏa mãn điểm (B) nằm trong góc (MAO) và (widehat {MAB} = frac{1}{2}widehat {AOB}). Chứng minh đường thẳng (MA) là tiếp tuyến của đường tròn (left( O right)).
Giải bài tập 1 trang 109 SGK Toán 9 tập 1 - Cánh diều
Ròng rọc là một loại máy cơ đơn giản có rãnh và có thể quay quanh một trục, được sử dụng rộng rãi trong công việc nâng lên và hạ xuống vật nặng trong cuộc sống. Trong Hình 41a, có một sợi dây không dãn vắt qua ròng rọc. Giả sử ròng rọc được minh họa bởi đường tròn (left( O right)), sợi dây vắt qua ròng rọc được minh hoạ bởi cung (MtN) và hai tiếp tuyến (Ma,Nb) của đường tròn (left( O right)) (Hình 41b). Chứng minh (Ma//Nb).
Giải mục 2 trang 108, 109 SGK Toán 9 tập 1 - Cánh diều
Cho đường tròn (left( {O;R} right)). Các đường thẳng (c,d) lần lượt tiếp xúc với đường tròn (left( {O;R} right)) tại (A,B) và cắt nhau tại (M) (Hình 38). a) Các tam giác (MOA) và (MOB) có bằng nhau hay không? b) Hai đoạn thẳng (MA) và (MB) có bằng nhau hay không? c) Tia (MO) có phải là tia phân giác của góc (AMB) hay không? d) Tia (OM) có phải là tia phân giác của gics (AOB) hay không?
Giải mục 1 trang 106, 107 SGK Toán 9 tập 1 - Cánh diều
Cho đường thẳng (a) là tiếp tuyến của đường tròn (left( {O;R} right)). Gọi (H) là hình chiếu của tâm (O) trên đường thẳng (a) (Hình 33). a) So sánh khoảng cách (OH) từ tâm (O) đến đường thẳng (a) và bán kính (R). b) Điểm (H) có thuộc đường tròn (left( {O;R} right)) hay không? c) Điểm (H) có phải là tiếp điểm của đường thẳng (a) và đường tròn (left( {O;R} right)) hay không? d) Đường thẳng (a) có vuông góc với bán kính đi qua tiếp điểm hay không?
Lý thuyết Tiếp tuyến của đường tròn Toán 9 Cánh diều
1. Nhận biết tiếp tuyến của đường tròn Nhận xét: Nếu một đường thẳng là tiếp tuyến của một đường tròn thì đường thẳng đó vuông góc với bán kính đi qua tiếp điểm.