-
Giải Toán 12 tập 1 - Cánh diều
-
Giải Toán 12 tập 2 - Cánh diều
Giải bài tập 15 trang 83 SGK Toán 12 tập 1 - Cánh diều
Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0;0;6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là ({A_1}(0;1;0)), ({A_2}(frac{{sqrt 3 }}{2}; - frac{1}{2};0)), ({A_3}( - frac{{sqrt 3 }}{2}; - frac{1}{2};0)) (Hình 40). Biết rằng trọng lượng của chiếc máy là 300N. Tìm tọa độ của các lực tác dụng lên giá đỡ (overrightarrow {{F_1}} ,overrightarrow {{F_2}} ,overrightarrow {{F_3}} )
Đề bài
Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0;0;6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \({A_1}(0;1;0)\), \({A_2}(\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)\), \({A_3}( - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)\) (Hình 40). Biết rằng trọng lượng của chiếc máy là 300N. Tìm tọa độ của các lực tác dụng lên giá đỡ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \)
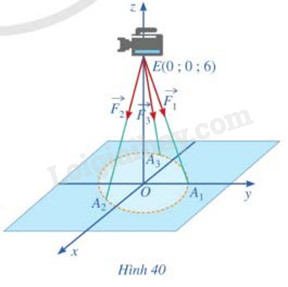
Phương pháp giải - Xem chi tiết
Vì đèn cân bằng nên trọng lực của đèn sẽ phân bố đều trên các chân của giá đỡ. Từ tọa độ các điểm đã cho, ta tìm được cái mối liên hệ với vecto lực và tìm được tọa độ của các vecto lực
Lời giải chi tiết
Ta có:
\(\left| {\overrightarrow {{A_1}O} } \right| = \sqrt {{{(0 - 0)}^2} + {{(1 - 0)}^2} + {{(0 - 0)}^2}} = 1\);
\(\left| {\overrightarrow {{A_2}O} } \right| = \sqrt {{{\left( {\frac{{\sqrt 3 }}{2} - 0} \right)}^2} + {{\left( { - \frac{1}{2} - 0} \right)}^2} + {{(0 - 0)}^2}} = 1\);
\(\left| {\overrightarrow {{A_3}O} } \right| = \sqrt {{{\left( { - \frac{{\sqrt 3 }}{2} - 0} \right)}^2} + {{\left( { - \frac{1}{2} - 0} \right)}^2} + {{(0 - 0)}^2}} = 1\).
Do đó \({A_1}O = {A_2}O = {A_3}O = 1\), suy ra O là trọng tâm tam giác \({A_1}{A_2}{A_3}\).
Khi đó \(\overrightarrow {E{A_1}} + \overrightarrow {E{A_2}} + \overrightarrow {E{A_3}} = 3\overrightarrow {EO} \) (tính chất trọng tâm).
Mặt khác, dễ dàng chứng minh độ dài các giá đỡ \(E{A_1} = E{A_2} = E{A_3}\) (do các tam giác vuông \(EO{A_1}\), \(EO{A_2}\), \(EO{A_3}\) bằng nhau). Các lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) cùng phương với các giá đỡ và có độ lớn bằng nhau nên ta có tỉ lệ:
\(\frac{{\left| {\overrightarrow {{F_1}} } \right|}}{{E{A_1}}} = \frac{{\left| {\overrightarrow {{F_2}} } \right|}}{{E{A_2}}} = \frac{{\left| {\overrightarrow {{F_3}} } \right|}}{{E{A_3}}} = k\) và \(\overrightarrow {{F_1}} = k\overrightarrow {E{A_1}} \), \(\overrightarrow {{F_2}} = k\overrightarrow {E{A_2}} \), \(\overrightarrow {{F_3}} = k\overrightarrow {E{A_3}} \).
Từ \(\overrightarrow {E{A_1}} + \overrightarrow {E{A_2}} + \overrightarrow {E{A_3}} = 3\overrightarrow {EO} \) đã chứng minh, ta được:
\(k\overrightarrow {E{A_1}} + k\overrightarrow {E{A_2}} + k\overrightarrow {E{A_3}} = 3k\overrightarrow {EO} \)
\( \Leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = 3k\overrightarrow {EO} \).
Mà \(\overrightarrow {EO} = (0 - 0;0 - 0;0 - 6) = (0;0 - 6)\).
Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = (0;0; - 18k)\).
Giả sử \(\overrightarrow P \) là trọng lực tác động lên cả 3 giá đỡ. \(\overrightarrow P \) là lực vuông góc với mặt phẳng (Oxy), hướng xuống dưới (ngược chiều với trục Oz) nên tọa độ của \(\overrightarrow P = (0;0; - 300)\).
Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \Leftrightarrow - 18k = - 300 \Leftrightarrow k = \frac{{50}}{3}\).
Vậy \(\overrightarrow {{F_1}} = (0;\frac{{50}}{3}; - 100)\); \(\overrightarrow {{F_2}} = (\frac{{25\sqrt 3 }}{3}; - \frac{{25}}{3}; - 100)\); \(\overrightarrow {{F_3}} = ( - \frac{{25\sqrt 3 }}{3}; - \frac{{25}}{3}; - 100)\).
Bình luận
Chia sẻ- Giải bài tập 14 trang 83 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 13 trang 83 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 12 trang 83 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 11 trang 83 SGK Toán 12 tập 1 - Cánh diều
- Giải bài tập 10 trang 82 SGK Toán 12 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Cánh diều - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
