Giải bài 9.52 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2

Cho tam giác nhọn ABC (AB<AC) có các đường cao AD, BE, CF. Cho EF cắt BC tại K. Chứng minh rằng: a) KB. KC = KE. KF; b) (frac{{KB}}{{KC}} = frac{{DB}}{{DC}}).

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Cho tam giác nhọn ABC (AB<AC) có các đường cao AD, BE, CF. Cho EF cắt BC tại K. Chứng minh rằng:

a) KB. KC = KE. KF;

b) $\frac{{KB}}{{KC}} = \frac{{DB}}{{DC}}$.

Phương pháp giải - Xem chi tiết

a) + Chứng minh tứ BFEC nội tiếp đường tròn đường kính BC, suy ra $\widehat {KFB} = {180^o} - \widehat {BFE} = \widehat {BCE}$.

+ Chứng minh $\Delta KFB\backsim \Delta KCE\left( g.g \right)$, suy ra KB. KC = KE. KF.

b) + Chứng minh $\Delta KEB\backsim \Delta KCF\left( g.g \right)$, suy ra $\frac{{KE}}{{KC}} = \frac{{EB}}{{CF}}$.

+ Chứng minh $\frac{{KB}}{{KE}} = \frac{{FB}}{{CE}}$ suy ra $\frac{{KB}}{{KC}} = \frac{{KB}}{{KE}}.\frac{{KE}}{{KC}} = \frac{{BF}}{{CF}}.\frac{{BE}}{{CE}}$ (1)

+ Chứng minh $\Delta BDF\backsim \Delta BAC\left( g.g \right)$ nên $\frac{{DB}}{{AB}} = \frac{{BF}}{{BC}}$, tương tự ta có $\frac{{DC}}{{AC}} = \frac{{CE}}{{BC}}$ nên $\frac{{DB}}{{DC}} = \frac{{BF}}{{CE}}.\frac{{AB}}{{AC}}$ (2)

+ Chứng minh $\Delta ABE\backsim \Delta ACF$, suy ra $\frac{{AB}}{{AC}} = \frac{{BE}}{{CF}}$ (3).

+ Từ (1), (2) và (3) suy ra điều phải chứng minh.

Lời giải chi tiết

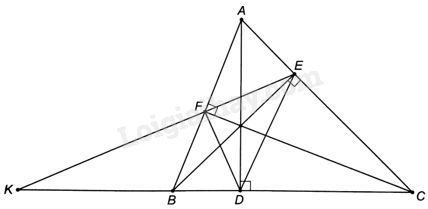
a) Vì $\widehat {BFC} = \widehat {BEC} = {90^o}$ nên tứ giác BFEC nội tiếp đường tròn đường kính BC.

Chứng minh tương tự ta có: tứ giác AFDC nội tiếp đường tròn đường kính AC, tứ giác AEDB nội tiếp đường tròn đường kính AB.

Vì tứ giác BFEC nội tiếp đường tròn đường kính BC nên $\widehat {KFB} = {180^o} - \widehat {BFE} = \widehat {BCE}$.

Tam giác KFB và tam giác KCE có: $\widehat {KFB} = \widehat {BCE}$, góc K chung.

Suy ra: $\Delta KFB\backsim \Delta KCE\left( g.g \right)$. Suy ra, $\frac{{KF}}{{KC}} = \frac{{KB}}{{KE}}$, hay KB. KC = KE. KF.

b) Hai tam giác KEB và tam giác KCF có: $\widehat {KEB} = \widehat {KCF}$ (hai góc nội tiếp cùng chắn cung BF của đường tròn đường kính BC), góc K chung nên $\Delta KEB\backsim \Delta KCF\left( g.g \right)$, suy ra $\frac{{KE}}{{KC}} = \frac{{EB}}{{CF}}$.

Mặt khác: $\frac{{KB}}{{KE}} = \frac{{FB}}{{CE}}$ (do $\Delta KFB\backsim \Delta KCE\left( cmt \right)$). Suy ra: $\frac{{KB}}{{KC}} = \frac{{KB}}{{KE}}.\frac{{KE}}{{KC}} = \frac{{BF}}{{CF}}.\frac{{BE}}{{CE}}$ (1)

Chứng minh tương tự ta có: hai tam giác BDF và tam giác BAC có:

$\widehat {BDF} = {180^o} - \widehat {FDC} = \widehat {BAC};\widehat {DBF} = \widehat {ABC}$.

Suy ra: $\Delta BDF\backsim \Delta BAC\left( g.g \right)$, suy ra $\frac{{DB}}{{AB}} = \frac{{BF}}{{BC}}$. Tương tự ta có: $\frac{{DC}}{{AC}} = \frac{{CE}}{{BC}}$ nên $\frac{{DB}}{{DC}} = \frac{{BF}}{{CE}}.\frac{{AB}}{{AC}}$ (2)

Mà $\Delta ABE\backsim \Delta ACF$ (hai tam giác vuông có chung góc nhọn BAC). Do đó, $\frac{{AB}}{{AC}} = \frac{{BE}}{{CF}}$ (3).

Từ (1), (2) và (3) ta có: $\frac{{KB}}{{KC}} = \frac{{DB}}{{DC}}$.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 9.53 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho một lục giác đều và một tam giác đều cùng nội tiếp một đường tròn. Biết rằng tam giác đều có cạnh bằng 3cm. Tính chu vi và diện tích của hình lục giác đều đã cho.
Giải bài 9.54 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho đa giác đều H có 12 cạnh, nội tiếp một đường tròn (O). Kẻ các đoạn thẳng nối O với các đỉnh của H và thu được 12 góc nhọn tại đỉnh O (không chồng lên nhau). a) Chứng tỏ rằng mỗi góc nhọn này có số đo bằng ({30^o}). b) Hãy chỉ ra 12 phép quay giữ nguyên H.
Giải bài 9.51 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác nhọn ABC có đường cao AH. Các điểm M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Chứng minh rằng (AM.AB = AN.AC).
Giải bài 9.50 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Hãy cho biết số đo các góc còn lại của tứ giác nội tiếp ABCD trong mỗi trường hợp sau: a) (widehat A = {80^o},widehat D = {100^o}); b) (widehat B = {80^o},widehat A = {110^o}); c) (widehat C = {120^o},widehat B = {60^o}); d) (widehat D = {65^o},widehat C = {125^o}).
Giải bài 9.49 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác ABC vuông tại A, có diện là (24c{m^2}) và nội tiếp đường tròn có bán kính 5cm. Tính bán kính đường tròn nội tiếp tam giác ABC.
Giải bài 9.48 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Tính diện tích tam giác vuông cân, nội tiếp đường tròn bán kính 4cm.
Giải bài 9.47 trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác đều ABC nội tiếp một đường tròn bán kính 4cm. Hãy tính độ dài mỗi cạnh và bán kính đường tròn nội tiếp của tam giác ABC.
Giải bài 9.46 trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác ABC ngoại tiếp đường tròn (I). Đường tròn (I) tiếp xúc các cạnh BC, CA, AB tại D, E, F. Chứng tỏ rằng IEAF, IFBD, IDCE là các tứ giác nội tiếp.
Giải bài 9.45 trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Tính số đo của các góc BOC, COA, AOB, biết rằng (widehat A = {60^o},widehat B = {70^o}).
Giải bài 9.44 trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Xét trong một đường tròn, những câu nào dưới đây là đúng? a) Hai góc nội tiếp bằng nhau chắn hai cung bằng nhau. b) Hai góc ở tâm bằng nhau chắn hai cung bằng nhau. c) Góc ở tâm có số đo bằng góc nội tiếp chắn cùng một cung. d) Góc nội tiếp có số đo bằng số đo cung bị chắn.
Giải câu hỏi trắc nghiệm trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tứ giác ABCD nội tiếp một đường tròn với (widehat A = {70^o},widehat B = {100^o}). Khẳng định nào dưới đây là đúng? A. (widehat C = {80^o},widehat D = {110^o}). B. (widehat C = {110^o},widehat D = {80^o}). C. (widehat C = {140^o},widehat D = {200^o}). D. (widehat C = {200^o},widehat D = {140^o}).