Giải bài 9.49 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2

Cho tam giác ABC vuông tại A, có diện là (24c{m^2}) và nội tiếp đường tròn có bán kính 5cm. Tính bán kính đường tròn nội tiếp tam giác ABC.

Đề bài

Cho tam giác ABC vuông tại A, có diện là \(24c{m^2}\) và nội tiếp đường tròn có bán kính 5cm. Tính bán kính đường tròn nội tiếp tam giác ABC.

Phương pháp giải - Xem chi tiết

+ Tính BC, áp dụng định lí Pythagore vào tam giác ABC vuông tại A tính được \(A{C^2} + A{B^2}\).

+ Tính được \(AB.AC\).

+ Vì \({\left( {AB + AC} \right)^2} = A{B^2} + 2AB.AC + A{C^2}\) nên tính được \(AB + AC\).

+ Gọi I là tâm đường tròn nội tiếp và r là bán kính của đường tròn nội tiếp tam giác ABC.

+ Ta có:

\(S = {S_{AIB}} + {S_{AIC}} + {S_{BIC}} = \frac{1}{2}r\left( {AB + BC + CA} \right)\), từ đó tính được r.

Lời giải chi tiết

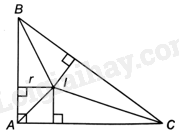
Vì bán kính đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền nên \(BC = 2.5 = 10\left( {cm} \right)\).

Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có: \(A{C^2} + A{B^2} = B{C^2} = 100\).

Vì tam giác ABC có diện là \(24c{m^2}\) nên:

\(\frac{1}{2}AB.AC = 24\) hay \(AB.AC = 48\).

Ta có:

\({\left( {AB + AC} \right)^2} = A{B^2} + 2AB.AC + A{C^2} = 196\),

suy ra \(AB + AC = 14cm\).

Gọi I là tâm đường tròn nội tiếp và r là bán kính của đường tròn nội tiếp tam giác ABC.

Khi đó, r cũng là chiều cao hạ từ đỉnh I xuống các cạnh BC, CA, AB của các tam giác BIC, CIA, ABI.

Ta có: \(S = {S_{AIB}} + {S_{AIC}} + {S_{BIC}} = \frac{1}{2}r\left( {AB + BC + CA} \right)\), suy ra:

\(r = \frac{{2S}}{{AB + BC + AC}} = \frac{{48}}{{10 + 14}} = 2\left( {cm} \right).\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 9.50 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Hãy cho biết số đo các góc còn lại của tứ giác nội tiếp ABCD trong mỗi trường hợp sau: a) (widehat A = {80^o},widehat D = {100^o}); b) (widehat B = {80^o},widehat A = {110^o}); c) (widehat C = {120^o},widehat B = {60^o}); d) (widehat D = {65^o},widehat C = {125^o}).
Giải bài 9.51 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác nhọn ABC có đường cao AH. Các điểm M và N lần lượt là hình chiếu vuông góc của H trên AB, AC. Chứng minh rằng (AM.AB = AN.AC).
Giải bài 9.52 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác nhọn ABC (AB
Giải bài 9.53 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho một lục giác đều và một tam giác đều cùng nội tiếp một đường tròn. Biết rằng tam giác đều có cạnh bằng 3cm. Tính chu vi và diện tích của hình lục giác đều đã cho.
Giải bài 9.54 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho đa giác đều H có 12 cạnh, nội tiếp một đường tròn (O). Kẻ các đoạn thẳng nối O với các đỉnh của H và thu được 12 góc nhọn tại đỉnh O (không chồng lên nhau). a) Chứng tỏ rằng mỗi góc nhọn này có số đo bằng ({30^o}). b) Hãy chỉ ra 12 phép quay giữ nguyên H.
Giải bài 9.48 trang 62 sách bài tập toán 9 - Kết nối tri thức tập 2
Tính diện tích tam giác vuông cân, nội tiếp đường tròn bán kính 4cm.
Giải bài 9.47 trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác đều ABC nội tiếp một đường tròn bán kính 4cm. Hãy tính độ dài mỗi cạnh và bán kính đường tròn nội tiếp của tam giác ABC.
Giải bài 9.46 trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác ABC ngoại tiếp đường tròn (I). Đường tròn (I) tiếp xúc các cạnh BC, CA, AB tại D, E, F. Chứng tỏ rằng IEAF, IFBD, IDCE là các tứ giác nội tiếp.
Giải bài 9.45 trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Tính số đo của các góc BOC, COA, AOB, biết rằng (widehat A = {60^o},widehat B = {70^o}).
Giải bài 9.44 trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Xét trong một đường tròn, những câu nào dưới đây là đúng? a) Hai góc nội tiếp bằng nhau chắn hai cung bằng nhau. b) Hai góc ở tâm bằng nhau chắn hai cung bằng nhau. c) Góc ở tâm có số đo bằng góc nội tiếp chắn cùng một cung. d) Góc nội tiếp có số đo bằng số đo cung bị chắn.
Giải câu hỏi trắc nghiệm trang 61 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tứ giác ABCD nội tiếp một đường tròn với (widehat A = {70^o},widehat B = {100^o}). Khẳng định nào dưới đây là đúng? A. (widehat C = {80^o},widehat D = {110^o}). B. (widehat C = {110^o},widehat D = {80^o}). C. (widehat C = {140^o},widehat D = {200^o}). D. (widehat C = {200^o},widehat D = {140^o}).