-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
SBT Toán 8 - giải SBT Toán 8 - Kết nối tri thức với cuộc sống
Bài 34. Ba trường hợp đồng dạng của hai tam giác - SBT ..
Giải bài 9.25 trang 56 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho hình thang ABCD (AB//CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F.
Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho hình thang ABCD (AB//CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F.
a) Chứng minh rằng: $\Delta EAB\backsim \Delta EDC,\Delta FAB\backsim \Delta FCD$.
b) Lấy hai điểm M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, E, F thẳng hàng.
Phương pháp giải - Xem chi tiết
a) + Sử dụng kiến thức định lí (một trường hợp đặc biệt của hai tam giác đồng dạng) để chứng minh $\Delta EAB\backsim \Delta EDC$: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh $\Delta FAB\backsim \Delta FCD$: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc): Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) Để chứng minh 4 điểm M, N, E, F thẳng hàng ta chứng minh:
+ Tia EM trùng với tia EN hay 3 điểm M, E, N thẳng hàng.
+ Tia FM và tia FN là hai tia đối nhau hay F, M, N thẳng hàng.
Lời giải chi tiết
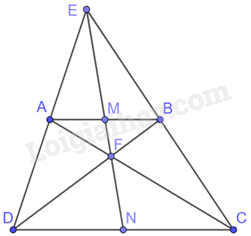
a) Tam giác EDC có: AB//CD nên $\Delta EAB\backsim \Delta EDC$
Vì AB//CD nên \(\widehat {BAC} = \widehat {ACD}\) hay \(\widehat {FAB} = \widehat {FCD}\)
Tam giác FAB và tam giác FCD có:
\(\widehat {BFA} = \widehat {CFD}\) (hai góc đối đỉnh), \(\widehat {FAB} = \widehat {FCD}\) (cmt)
Do đó, $\Delta FAB\backsim \Delta FCD\left( g-g \right)$
b) Vì $\Delta EAB\backsim \Delta EDC$(cmt) nên \(\frac{{EA}}{{ED}} = \frac{{AB}}{{DC}} = \frac{{AM}}{{DN}}\)
Tam giác EAM và tam giác EDN có:
\(\frac{{EA}}{{ED}} = \frac{{AM}}{{DN}}\) (cmt), \(\widehat {EAM} = \widehat {EDN}\) (AM//DN, hai góc đồng vị). Do đó, $\Delta EAM\backsim \Delta EDN\left( c-g-c \right)$
Suy ra: \(\widehat {AEM} = \widehat {DEN}\). Do đó, tia EM trùng với tia EN hay 3 điểm M, E, N thẳng hàng (1).
Vì nên \(\frac{{FA}}{{FC}} = \frac{{AB}}{{CD}} = \frac{{AM}}{{CN}}\)
Hai tam giác FAM và tam giác FCN có:
\(\frac{{FA}}{{FC}} = \frac{{AM}}{{CN}}\left( {cmt} \right)\), \(\widehat {FAM} = \widehat {FCN}\) (AM//CN, hai góc so le trong). Do đó, $\Delta FAM\backsim \Delta FCN\left( c-g-c \right)$ nên \(\widehat {AFM} = \widehat {CFN}\). Do đó, tia FM và tia FN là hai tia đối nhau. Suy ra, F, M, N thẳng hàng (2).
Từ (1) và (2) ta có: 4 điểm M, N, E, F thẳng hàng
Bình luận
Chia sẻ
- Giải bài 9.26 trang 56 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 9.27 trang 57 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 9.28 trang 57 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 9.29 trang 57 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 9.30 trang 57 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải bài 16 trang 83 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 15 trang 83 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 14 trang 83 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 13 trang 82 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 12 trang 82 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 16 trang 83 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 15 trang 83 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 14 trang 83 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 13 trang 82 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
- Giải bài 12 trang 82 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
