Giải bài 8 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2

Một thùng đựng rác có dạng hình chóp cụt tứ giác đều. Đáy và miệng thùng có độ dài lần lượt là 60cm và 120cm, cạnh bên của thùng dài 100cm. Tính thể tích của thùng.

Đề bài

Một thùng đựng rác có dạng hình chóp cụt tứ giác đều. Đáy và miệng thùng có độ dài lần lượt là 60cm và 120cm, cạnh bên của thùng dài 100cm. Tính thể tích của thùng.

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về thể tích khối chóp cụt đều: Hình chóp cụt đều có chiều cao h và diện tích hai đáy S, S’ là: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\)

Quảng cáo

Lời giải chi tiết

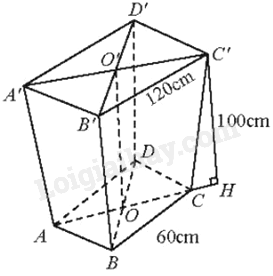
Đặt tên các điểm như hình vẽ.

Kẻ \(C'H \bot AC\left( {H \in AC} \right)\)

Ta có: \(O'C' \) \( = \frac{{\sqrt {{{120}^2} + {{120}^2}} }}{2} \) \( = 60\sqrt 2 \left( {cm} \right)\), \(OC \) \( = \frac{{\sqrt {{{60}^2} + {{60}^2}} }}{2} \) \( = 30\sqrt 2 \left( {cm} \right)\)

\( \Rightarrow CH \) \( = O'C' - OC \) \( = 30\sqrt 2 \)

Áp dụng công thức \(V \) \( = \frac{h}{3}\left( {S + \sqrt {S'S} + S'} \right)\)

Với \(h \) \( = C'H \) \( = \sqrt {CC{'^2} - C{H^2}} \) \( = \sqrt {{{100}^2} - {{\left( {30\sqrt 2 } \right)}^2}} \) \( = 10\sqrt {82} \left( {cm} \right)\), \(S \) \( = {120^2}\left( {c{m^2}} \right),S' \) \( = {60^2}\left( {c{m^2}} \right)\)

Vậy thể tích thùng là: \(V \) \( = \frac{{10\sqrt {82} }}{3}\left( {{{120}^2} + \sqrt {{{120}^2}{{.60}^2}} + {{60}^2}} \right) \) \( = 84000\sqrt {82} \left( {c{m^3}} \right)\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh 2a. Mặt phẳng (B’AC) tạo với đáy một góc \({30^0}\), khoảng cách từ B đến mặt phẳng (D’AC) bằng \(\frac{a}{2}\). Tính thể tích khối tứ diện ACB’D’.
Giải bài 6 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với \(AB = AC = a,\widehat {BAC} = {120^0}\),
Giải bài 5 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B. Biết \(AB = a,BC = a\sqrt 3 \),
Giải bài 4 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho khối chóp S.ABC có \(SA \bot \left( {ABC} \right)\), tam giác ABC có độ dài 3 cạnh là \(AB = 5a,BC = 8a,AC = 7a\), góc giữa SB và (ABC) là \({45^0}\). Tính thể tích khối chóp S.ABC.
Giải bài 3 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho hình chóp S. ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho \(HA = 2HB\).
Giải bài 2 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với (DBC). a) Chứng minh hai mặt phẳng (ABE) và (DFK) cùng vuông góc với (ADC). b) Gọi O và H là trực tâm \(\Delta BCD\) và \(\Delta ACD\).
Giải bài 1 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. a) \(BC \bot \left( {OAH} \right)\). b) H là trực tâm của \(\Delta ABC\). c) \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\).
Giải câu hỏi trắc nghiệm trang 74, 75 sách bài tập toán 11 - Chân trời sáng tạo tập 2
Trong không gian, khẳng định nào sau đây đúng? A. Cho hai đường thẳng song song, B. Trong không gian, C. Hai đường thẳng phân biệt vuông góc với nhau thì chúng cắt nhau. D. Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba