Giải bài 6 trang 75 vở thực hành Toán 7 tập 2

Cho tam giác ABC, điểm M nằm giữa B và C. Chứng minh rằng: (frac{1}{2}left( {AB - BC + CA} right) < AM).

Đề bài

Cho tam giác ABC, điểm M nằm giữa B và C. Chứng minh rằng:

\(\frac{1}{2}\left( {AB - BC + CA} \right) < AM\).

Phương pháp giải - Xem chi tiết

+ Chỉ ra \(AM > AB - BM\), \(AM > AC - CM\).

+ Cộng từng vế của hai bất đẳng thức trên suy ra điều phải chứng minh.

Lời giải chi tiết

(H.9.16)

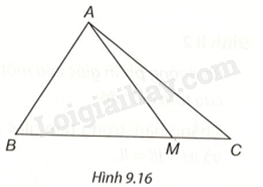
Trong tam giác ABM, ta có \(AM > AB - BM\) (1)

Trong tam giác ACM, ta có \(AM > AC - CM\) (2)

Từ (1) và (2), ta có:

\(2AM > AB - BM + AC - CM\) hay \(2AM > AB + AC - BC\)

Suy ra \(AM > \frac{1}{2}\left( {AB - BC + CA} \right)\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Giải bài 5 (9.18) trang 75 vở thực hành Toán 7 tập 2
Biết hai cạnh của tam giác có độ dài a và b. Dựa vào bất đẳng thức tam giác, hãy giải thích tại sao chu vi của tam giác đó lớn hơn 2a và nhỏ hơn (2left( {a + b} right)).
Giải bài 4 (9.17) trang 74, 75 vở thực hành Toán 7 tập 2
Độ dài hai cạnh của một tam giác bằng 7cm và 2cm. Tìm độ dài cạnh còn lại biết rằng số đo của nó theo xentimét là một số tự nhiên lẻ.
Giải bài 3 (9.16) trang 74 vở thực hành Toán 7 tập 2
Tính chu vi của tam giác cân biết hai cạnh của nó có độ dài là 2cm và 5cm.
Giải bài 2 (9.15) trang 74 vở thực hành Toán 7 tập 2
Hỏi có tam giác nào với độ dài ba cạnh là 2,5cm; 3,4cm và 6cm không? Vì sao?
Giải bài 1 (9.14) trang 74 vở thực hành Toán 7 tập 2
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.15).