-
Toán 8 tập 1 - Chân trời sáng tạo
-
Toán 8 tập 2 - Chân trời sáng tạo
Giải bài 6 trang 67 SGK Toán 8 – Chân trời sáng tạo
Ta gọi tứ giác ABCD với
Đã có lời giải SGK Toán lớp 9 - Chân trời sáng tạo (mới)
Đầy đủ - Chi tiết - Chính xác
Đề bài
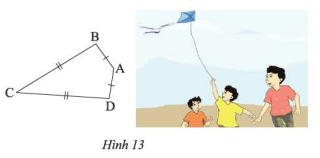
Ta gọi tứ giác ABCD với AB = AD, CB = CD (hình 13) là hình “cái diều”.
a. Chứng minh rằng AC là đường trung trực của BD.
b. Cho biết \(\widehat B = {95^0},\widehat C = {35^0}.\)Tính \(\widehat A\) và \(\widehat D\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Sử dụng tính chất của đường trung trực để chứng minh \(AC\) là trung trực của \(BD\)
b) Sử dụng tính chất tổng bốn góc trong tứ giác \(ABCD\)
Lời giải chi tiết
a) Ta có:
\(AB = AD\) (gt) nên \(A\) thuộc đường trung trực của \(BD\)
\(CB = CD\) (gt) nên \(C\) thuộc đường trung trực của \(BD\)
Vậy \(AC\) là đường trung trực của \(BD\)
b) Xét \(\Delta ABC\) và \(\Delta ADC\) ta có:
\(AB = AD\) (gt)
\(BC = CD\) (gt)
\(AC\) chung
Suy ra: \(\Delta ABC = \Delta ADC\) (c-g-c)
Suy ra: \(\widehat {ABC} = \widehat {ADC} = 95^\circ \) (hai góc tương ứng)
Trong tứ giác \(ABCD\), tổng các góc bằng \(360^\circ \) nên:
\(\widehat A = 360^\circ - \left( {95^\circ + 35^\circ + 95^\circ } \right) = 135^\circ \)
Bình luận
Chia sẻ
- Giải bài 7 trang 67 SGK Toán 8 – Chân trời sáng tạo
- Giải bài 5 trang 67 SGK Toán 8 – Chân trời sáng tạo
- Giải bài 4 trang 67 SGK Toán 8 – Chân trời sáng tạo
- Giải bài 3 trang 67 SGK Toán 8 – Chân trời sáng tạo
- Giải bài 2 trang 66 SGK Toán 8 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Xác suất lí thuyết và xác suất thực nghiệm SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Mô tả xác suất bằng tỉ số SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Hai hình đồng dạng SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Chân trời sáng tạo
- Lý thuyết Các trường hợp đồng dạng của hai tam giác SGK Toán 8 - Chân trời sáng tạo
