Giải bài 5 trang 88, 89 vở thực hành Toán 7 tập 2

Đề bài

Cho tam giác ABC cân tại A. Trên tia đối của tia BC và tia đối của tia CB theo thứ tự lấy hai điểm D và E sao cho $BD = CE$.

a) Chứng minh $\Delta ADE$ cân.

b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của góc DAE và $AM \bot DE$.

c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD, AE. Chứng minh: $BH = CK$.

d) Chứng minh: HK//BC.

Lời giải chi tiết

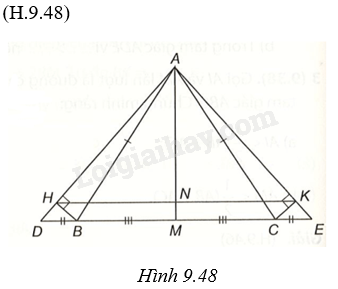
a) Do $\Delta ABC$ cân tại A nên $\widehat {ABC} = \widehat {ACB}$, suy ra $\widehat {ABD} = \widehat {ACE}$ (cùng bù với góc ABC, ACB).

Xét $\Delta ABD$ và $\Delta ACE$ có:

$AB = AC$ (do tam giác ABC cân tại A), $\widehat {ABD} = \widehat {ACE}$ (chứng minh trên), $BD = CE$ (theo giả thiết), suy ra $\Delta ABD = \Delta ACE$ (c.g.c), do đó $AD = AE$ (hai cạnh tương ứng), suy ra $\Delta ADE$ cân tại A.

b) Ta có: $DM = DB + BM,EM = CE + MC$, mà $BD = CE$ (gt), $BM = MC$ (M là trung điểm của BC), suy ra $DM = MC$.

Xét $\Delta AMD$ và $\Delta AME$ có:

AM chung, $AD = AE$ (chứng minh trên), $DM = MC$ (chứng minh trên)

Do đó $\Delta AMD = \Delta AME$ (c.c.c), suy ra $\widehat {DAM} = \widehat {MAE}$ và $\widehat {DMA} = \widehat {EMA}$, suy ra AM là phân giác của góc DAE.

Mặt khác do $\widehat {DMA}$ và $\widehat {AME}$ là hai góc bù nhau nên $\widehat {DMA} = \widehat {AME} = {90^o}$ $AM \bot DE$.

c) Vì $\Delta ABD = \Delta ACE$ (chứng minh trên) nên $\widehat {DAB} = \widehat {CAE}$.

Xét tam giác vuông ABH và tam giác vuông ACK, ta có: $\widehat {DAB} = \widehat {CAE},AB = AC$ nên $\Delta ABH = \Delta ACK$ (cạnh huyền- góc nhọn), suy ra $BH = CK$ (hai cạnh tương ứng).

d) Gọi giao điểm của AM và HK là N.

Xét  $\Delta ANH$ và $\Delta ANK$, có: $AH = AK$ (do $\Delta ABH = \Delta ACK$), $\widehat {DAM} = \widehat {MAE}$ (chứng minh trên), AN là cạnh chung. Do đó, $\Delta ANH = \Delta ANK\left( {c.g.c} \right)$, suy ra $\widehat {ANH} = \widehat {ANK}$ (hai góc tương ứng), mà hai góc này kề bù nên $\widehat {ANH} = \widehat {ANK} = {90^o}$, suy ra $AM \bot HK$.

Ta có $AM \bot HK$, mà $AM \bot DE$ nên HK//BC.