Giải bài 4 trang 104 vở thực hành Toán 9 tập 2

Cho hình thoi ABCD có (widehat A = {60^o}). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.

Đề bài

Cho hình thoi ABCD có \(\widehat A = {60^o}\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.

Phương pháp giải - Xem chi tiết

+ Theo hình vẽ, ta thấy\(MBNPDQ\) là lục giác lồi.

+ Gọi \(a\) là độ dài cạnh hình thoi thì \(BM = BN = DP = DQ = \frac{a}{2}.\)

+ Chứng minh tam giác AMQ và CNP là các tam giác đều nên \(MQ = AM,\,\,NP = CP\), \(\widehat {QMB} = {180^{\rm{o}}} - \widehat {QMA} = {120^{\rm{o}}}.\)

+ Chứng minh tương tự \(\widehat {BNP} = \widehat {NPD} = \widehat {DQM} = {120^{\rm{o}}}.\)

+ Vì \(ABCD\) là hình thoi nên \(\widehat {MBN} = \widehat {PDQ} = {180^{\rm{o}}} - \widehat A\).

+ \(MBNPDQ\) là lục giác lồi có tất cả các cạnh và các góc bằng nhau và do đó là lục giác đều.

Lời giải chi tiết

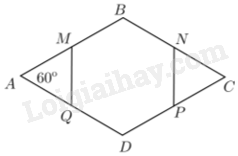
Theo hình vẽ, ta thấy\(MBNPDQ\) là lục giác lồi. Gọi \(a\) là độ dài cạnh hình thoi. Như vậy: \(BM = BN = DP = DQ = \frac{a}{2}.\)

Mặt khác, các tam giác cân \(AMQ\) và \(CNP\) có \(\widehat A = \widehat C = {60^{\rm{o}}}\) nên chúng là tam giác đều.

Do đó \(MQ = AM = \frac{a}{2},\,\,NP = CP = \frac{a}{2}.\) Hơn nữa \(\widehat {QMB} = {180^{\rm{o}}} - \widehat {QMA} = {120^{\rm{o}}}.\)

Tương tự, \(\widehat {BNP} = \widehat {NPD} = \widehat {DQM} = {120^{\rm{o}}}.\)

Vì \(ABCD\) là hình thoi nên \(\widehat {MBN} = \widehat {PDQ} = {180^{\rm{o}}} - \widehat A = {120^{\rm{o}}}.\) Vậy \(MBNPDQ\) là lục giác lồi có tất cả các cạnh và các góc bằng nhau và do đó là lục giác đều.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5 trang 104, 105 vở thực hành Toán 9 tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O) như hình bên. Phép quay ngược chiều ({60^o}) tâm O biến các điểm A, B, C lần lượt thành các điểm D, E, F. Chứng minh rằng ADBECF là một lục giác đều.
Giải bài 6 trang 105 vở thực hành Toán 9 tập 2
Liệt kê năm phép quay giữ nguyên một ngũ giác đều nội tiếp một đường tròn tâm O.
Giải bài 7 trang 105 vở thực hành Toán 9 tập 2
Cho vòng quay mặt trời gồm tám cabin như hình bên. Hỏi để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay thuận chiều quay của kim đồng hồ quanh tâm bao nhiêu độ?
Giải bài 8 trang 105, 106 vở thực hành Toán 9 tập 2
Cho ngũ giác đều ABCDE có các cạnh bằng 4cm nội tiếp một đường tròn (O). a) Tính bán kính của (O) biết rằng ta lấy (cos {54^o} approx 0,59). b) Liệt kê năm phép quay ngược chiều giữ nguyên ngũ giác đều ABCDE.
Giải bài 9 trang 106 vở thực hành Toán 9 tập 2
Cho tam giác ABC và O là trung điểm của cạnh AB. a) Tìm một phép quay tâm O biến điểm A thành điểm B và biến điểm B thành điểm A. b) Phép quay trên biến điểm C thành điểm D. Hãy chứng tỏ rằng ACBD là một hình bình hành.
Giải bài 3 trang 104 vở thực hành Toán 9 tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2cm. Tính độ dài các cạnh của tam giác ABC.
Giải bài 2 trang 103, 104 vở thực hành Toán 9 tập 2
Trong các hình dưới đây, hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều ({60^o}) tâm O biến điểm M thành điểm N?
Giải bài 1 trang 103 vở thực hành Toán 9 tập 2
Trong các hình phẳng sau, hình nào là hình phẳng có dạng đa giác đều?
Giải câu hỏi trắc nghiệm trang 103 vở thực hành Toán 9 tập 2
Khẳng định nào dưới đây là không đúng? A. Đa giác đều có các cạnh bằng nhau. B. Đa giác có các cạnh bằng nhau là đa giác đều. C. Đa giác đều có các góc bằng nhau. D. Đa giác đều nội tiếp được một đường tròn.