Giải bài 3 trang 120, 121 vở thực hành Toán 9

Đề bài

Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (P khác A và B) cắt xx’ tại M và cắt yy’ tại N.

a) Chứng minh rằng \(MN = MA + NB\).

b) Đường thẳng đi qua O và vuông góc với AB cắt MN tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.

c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.

Lời giải chi tiết

(H.5.40)

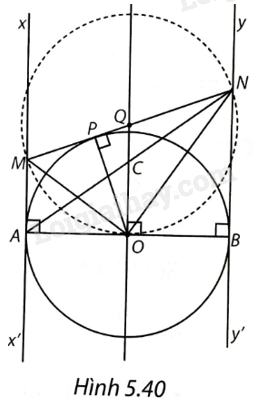
a) Ta có: $MN=MP+PN$. Mặt khác MA và MP là hai tiếp tuyến cắt nhau của (O) nên $MA=MP$.

Tương tự, ta cũng có $NB=NP$. Cộng từng vế hai đẳng thức trên ta được: $MA+NB=MP+PN=MN$ (điều phải chứng minh).

b) Do \(QO \bot AB\) (giả thiết), \(MA \bot AB\) và \(NB \bot AB\) (MA, NB là tiếp tuyến của (O) tại A và B) nên OQ//MA//NB. Nối A với N cắt OQ tại C.

Trong tam giác ABN, đường thẳng OQ đi qua trung điểm của cạnh AB và song song với BN nên C là trung điểm của AN.

Trong tam giác AMN, đường thẳng OQ đi qua trung điểm của AN và song song với AM nên Q là trung điểm của MN.

c) Theo tính chất của hai tiếp tuyến cắt nhau, OM là tia phân giác của góc AOP và ON là tia phân giác của góc POB. Khi đó:

\(\widehat {MON} = \widehat {MOP} + \widehat {NOP} \\= \frac{1}{2}\widehat {AOP} + \frac{1}{2}\widehat {BOP} \\= \frac{1}{2}\left( {\widehat {AOP} + \widehat {BOP}} \right) \\= \frac{1}{2}\widehat {AOB} = {90^o}\)

Do đó, tam giác MON là tam giác vuông tại O với OQ là đường trung tuyến. Từ đó ta có \(OQ = QN = QM\). Vậy đường tròn đường kính MN, cũng là đường tròn tâm Q đi qua O. Do đó, AB vuông góc với bán kính OQ tại O. Suy ra AB là tiếp tuyến của đường tròn đường kính MN.

Nói cách khác, AB tiếp xúc với đường tròn đường kính MN.