 SBT Toán 12 - giải SBT Toán 12 - Chân trời sáng tạo
SBT Toán 12 - giải SBT Toán 12 - Chân trời sáng tạo
 Bài tập cuối chương 1 - SBT Toán 12 Chân trời sáng tạo
Bài tập cuối chương 1 - SBT Toán 12 Chân trời sáng tạo
Giải bài 2 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
Người ta muốn làm một chiếc hộp hình hộp chữ nhật có đáy hình vuông và thể tích là \(10l\), Diện tích toàn phần nhỏ nhất của hộp là bao nhiêu?
Đề bài
Người ta muốn làm một chiếc hộp hình hộp chữ nhật có đáy hình vuông và thể tích là \(10l\), Diện tích toàn phần nhỏ nhất của hộp là bao nhiêu?
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính diện tích toàn phần hình hộp chữ nhật để tính diện tích toàn phần \(S\left( x \right)\), sau đó tìm giá trị nhỏ nhất của hàm số \(S\left( x \right)\).
Lời giải chi tiết
Giả sử cạnh của hộp là: \({\rm{x}}\left( {dm} \right)\), chiều cao của hộp là: \({\rm{h}}\left( {dm} \right)\).
Thể tích của hộp là: \(V = {x^2}.h = 10 \Leftrightarrow h = \frac{{10}}{{{x^2}}}\).
Diện tích toàn phần của hình hộp là \(S = 2{{\rm{x}}^2} + 4{\rm{x}}.h = 2{{\rm{x}}^2} + 4{\rm{x}}.\frac{{10}}{{{x^2}}} = 2{{\rm{x}}^2} + \frac{{40}}{x}\left( {d{m^2}} \right)\)
Xét hàm số \(S\left( x \right) = 2{{\rm{x}}^2} + \frac{{40}}{x}\) trên khoảng \(\left( {0; + \infty } \right)\).
Ta có: \(S'\left( x \right) = 4{\rm{x}} - \frac{{40}}{{{x^2}}};S'\left( x \right) = 0 \Leftrightarrow x = \sqrt[3]{{10}}\).
Bảng biến thiên:
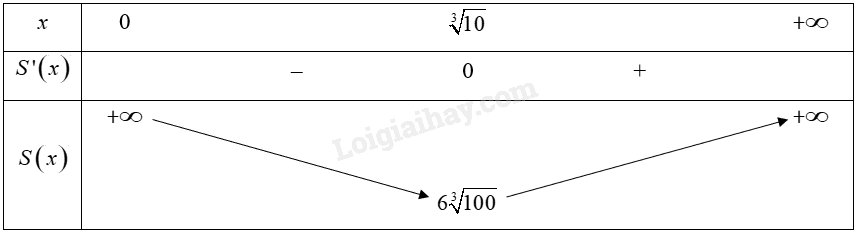
\(V\left( 0 \right) = 0;V\left( 2 \right) = 128;V\left( 6 \right) = 0\)
Vậy \(\mathop {\max }\limits_{\left[ {0;6} \right]} V\left( x \right) = V\left( 2 \right) = 128\).
Vậy với \(x = 2\left( {cm} \right)\) thì thể tích của hình hộp là lớn nhất.
- Giải bài 3 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 4 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 5 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 6 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 7 trang 37 sách bài tập toán 12 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 8 trang 37 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 7 trang 37 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 6 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 5 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 4 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 7 trang 87 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 6 trang 87 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 5 trang 87 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 4 trang 87 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 3 trang 87 sách bài tập toán 12 - Chân trời sáng tạo












Danh sách bình luận