Giải bài 17 trang 54 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho tam giác ABC vuông tại A, (AB = sqrt 2 ,AC = sqrt 6 ). Tính giá trị đúng (không làm trò) của a) Chu vi và diện tích tam giác ABC. b) Độ dài đường cao AH của tam giác ABC.
Đề bài
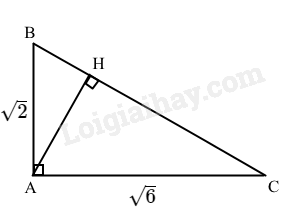
Cho tam giác ABC vuông tại A, \(AB = \sqrt 2 ,AC = \sqrt 6 \). Tính giá trị đúng (không làm trò) của
a) Chu vi và diện tích tam giác ABC.
b) Độ dài đường cao AH của tam giác ABC.
Phương pháp giải - Xem chi tiết
Dựa vào công thức chu vi tam giác ABC: \(P = AB + AC + BC;\)
diện tích tam giác ABC: \(S = \frac{1}{2}AB.AC\) .
Lời giải chi tiết
a) \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {2 + 6} = \sqrt 8 = 2\sqrt 2 .\)
Chu vi tam giác ABC là:
\(P = AB + AC + BC \\= \sqrt 2 + \sqrt 6 + 2\sqrt 2 = \sqrt 6 + 3\sqrt 2 .\)
Diện tích tam giác ABC là:
\(S = \frac{1}{2}AB.AC = \frac{1}{2}.\sqrt 2 .\sqrt 6 = \sqrt 3 \).
b) Ta có \(S = \frac{1}{2}BC.AH\)
suy ra \(AH = \frac{{2S}}{{BC}} = \frac{{2\sqrt 3 }}{{2\sqrt 2 }} = \frac{{\sqrt 6 }}{2}\).
- Giải bài 18 trang 54 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 19 trang 54 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 20 trang 54 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 21 trang 54 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 22 trang 54 sách bài tập toán 9 - Chân trời sáng tạo tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 4 trang 86 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 1 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 13 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 12 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2













Danh sách bình luận