Giải bài 10.15 trang 70 sách bài tập toán 9 - Kết nối tri thức tập 2

Một chiếc nón lá có dạng một hình nón không có đáy, đường kính đáy bằng 80cm, chiều cao bằng 30cm. Tính diện tích mặt ngoài của chiếc nón (làm tròn kết quả đến hàng đơn vị của (c{m^2})).

Đề bài

Một chiếc nón lá có dạng một hình nón không có đáy, đường kính đáy bằng 80cm, chiều cao bằng 30cm. Tính diện tích mặt ngoài của chiếc nón (làm tròn kết quả đến hàng đơn vị của \(c{m^2}\)).

Phương pháp giải - Xem chi tiết

Diện tích xung quanh của hình nón bán kính đáy r và độ dài đường sinh l là: \({S_{xq}} = \pi rl\).

Lời giải chi tiết

Đặt tên các điểm như hình vẽ.

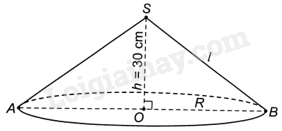
Bán kính đáy của hình nón là: \(R = OB = 80:2 = 40\left( {cm} \right)\).

Tam giác SOB vuông tại O nên theo định lí Pythagore ta có:

\(S{B^2} = S{O^2} + O{B^2} = 2\;500\) nên \(SB = 50m\).

Diện tích mặt ngoài của hình nón là:

\({S_{xq}} = \pi .OB.SB = 40.50.\pi = 2\;000\pi \left( {c{m^2}} \right) \approx 6\;283c{m^2}.\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 10.16 trang 70 sách bài tập toán 9 - Kết nối tri thức tập 2
Bạn Khôi có một chiếc bể cá làm bằng thủy tinh, có dạng hình cầu, đường kính 22cm. Khi nuôi cá, Khôi thường đổ vào bể lượng nước có thể tích bằng (frac{2}{3}) thể tích của bể. Tính thể tích nước bạn Khôi đổ vào bể khi nuôi cá (làm tròn kết quả đến hàng đơn vị của (c{m^3})).
Giải bài 10.17 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 2
Người ta cần làm một ống thoát nước hình trụ bằng bê tông (H.10.6) có chiều cao là 200cm, độ dày của thành ống là 15cm, đường kính của ống là 80cm. Tính lượng bê tông cần dùng để làm ống thoát nước nói trên.
Giải bài 10.18 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 2
Một hộp đựng bóng bàn có dạng hình trụ chứa vừa khít 3 quả bóng bàn có cùng bán kính R xếp theo chiều ngang (H.10.7). Gọi ({S_1}) là tổng diện tích của ba quả bóng bàn, ({S_2}) là diện tích xung quanh của vỏ hộp hình trụ. Tính tỉ số (frac{{{S_1}}}{{{S_2}}}).
Giải bài 10.19 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 2
Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1m, chiều cao bằng 2m. Người ta khoét từ hai đầu khối gỗ hai nửa hình cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu (H.10.8). Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu.
Giải bài 10.20 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 2
Một dụng gồm một phần có dạng hình trụ và một phần có dạng hình nón với kích thước như Hình 10.9. a) Tính thể tích của dụng cụ này. b) Tính diện tích mặt ngoài của dụng cụ (không tính nắp đậy, kết quả làm tròn đến hàng phần mười của ({m^2})).
Giải bài 10.14 trang 70 sách bài tập toán 9 - Kết nối tri thức tập 2
Một khối gỗ có dạng hình trụ, chiều cao bằng 50cm, đường kính đáy bằng 30cm. a) Tính thể tích của khối gỗ. b) Nếu sơn phủ kín mặt bên ngoài khối gỗ thì diện tích cần sơn là bao nhiêu (làm tròn kết quả đến hàng đơn vị của (c{m^2}))?
Giải câu hỏi trắc nghiệm trang 69, 70 sách bài tập toán 9 - Kết nối tri thức tập 2
Gọi h, R lần lượt là độ dài của chiều cao và bán kính đáy của hình trụ. Diện tích xung quanh của hình trụ là A. ({S_{xq}} = 2pi Rh). B. ({S_{xq}} = pi Rh). C. ({S_{xq}} = pi Rl). D. ({S_{xq}} = pi {R^2}h).