Giải bài 1 trang 62 sách bài tập toán 12 - Chân trời sáng tạo

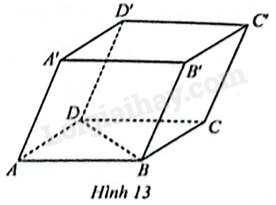
Cho hình hộp \(ABCD.A'B'C'D'\). a) Chỉ ra các vectơ có điểm đầu là \(B\) và điểm cuối là các đỉnh của hình hộp không cùng nằm trên một mặt của hình hộp với điểm \(B\). b) Tìm các vectơ bằng vectơ \(\overrightarrow {BC} \). c) Tìm các vectơ đối của vectơ \(\overrightarrow {BD} \).

Đề bài

Cho hình hộp \(ABCD.A'B'C'D'\).

a) Chỉ ra các vectơ có điểm đầu là \(B\) và điểm cuối là các đỉnh của hình hộp không cùng nằm trên một mặt của hình hộp với điểm \(B\).

b) Tìm các vectơ bằng vectơ \(\overrightarrow {BC} \).

c) Tìm các vectơ đối của vectơ \(\overrightarrow {BD} \).

Phương pháp giải - Xem chi tiết

Sử dụng khái niệm vectơ, vectơ bằng nhau, vectơ đối nhau.

Lời giải chi tiết

a) Vectơ có điểm đầu là \(B\) và điểm cuối là các đỉnh của hình hộp không cùng nằm trên một mặt của hình hộp với điểm \(B\) là: \(\overrightarrow {BD'} \).

b) Các vectơ bằng vectơ \(\overrightarrow {BC} \) là: \(\overrightarrow {AD} ,\overrightarrow {AD} ,\overrightarrow {BC} \).

c) Các vectơ đối của vectơ \(\overrightarrow {BD} \) là: \(\overrightarrow {DB} ,\overrightarrow {D'B} \).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 2 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Cho tứ diện \(OABC\). Tìm các vectơ: a) \(\overrightarrow {OA} + \overrightarrow {AB} - \overrightarrow {OC} \); b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} \).
Giải bài 3 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc \({120^ \circ }\) và có độ lớn lần lượt là \(10N\) và \(8N\). Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn \(6N\). Tính độ lớn của hợp lực của ba lực trên.
Giải bài 4 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AC'\) và \(A'C\) cắt nhau tại \(O\). Cho biết \(AO = a\). Tính theo \(a\) độ dài các vectơ: a) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \); b) \(\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {A'A} \).
Giải bài 5 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Cho hình lập phương \(ABCD.A'B'C'D'\). Gọi \(O,O'\)lần lượt là tâm của các hình vuông \(ABCD\) và \(A'B'C'D'\); \(I\) là giao điểm của \(AC'\) và \(A'C\). Chứng minh rằng: a) \(\overrightarrow {OA'} + \overrightarrow {OB'} + \overrightarrow {OC'} + \overrightarrow {OD'} = 4\overrightarrow {OO'} \); b) \(\overrightarrow {DB} + \overrightarrow {DD'} = 2\overrightarrow {DI} \).
Giải bài 6 trang 63 sách bài tập toán 12 - Chân trời sáng tạo
Cho hình hộp (ABCD.A'B'C'D') có tất cả các cạnh bằng (a) và cho biết (widehat {BAD} = widehat {BAA'} = widehat {DAA'} = {60^ circ }). Tính các tích vô hướng sau: a) (overrightarrow {AB} .overrightarrow {AD} ); b) (overrightarrow {DA} .overrightarrow {DC} ); c) (overrightarrow {AA'} .overrightarrow {AC} ).
Giải bài 7 trang 64 sách bài tập toán 12 - Chân trời sáng tạo
Một tàu kéo một xà lan trên biển di chuyển được 3 km với một lực kéo có cường độ 2000 N và có phương hợp với phương dịch chuyển một góc ({30^ circ }). Tính công thực hiện bởi lực kéo nói trên (kết quả làm tròn đến hàng đơn vị của Jun).
Giải bài 8 trang 64 sách bài tập toán 12 - Chân trời sáng tạo
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Gọi \(x,y,z\) theo thứ tự là số đo các góc hợp bởi vectơ \(\overrightarrow {AC'} \) với các vectơ \(\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {AA'} \). Chứng minh \({\cos ^2}x + {\cos ^2}y + {\cos ^2}z = 1\).
Giải bài 9 trang 64 sách bài tập toán 12 - Chân trời sáng tạo
Tính độ lớn của các lực căng trên mỗi sợi dây cáp trong Hình 16. Cho biết khối lượng xe là 1900 kg, gia tốc là 10 m/s, khung nâng có khối lượng 100 kg và có dạng hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình chữ nhật tâm \(O\), \(AB=8m,BC=12m,SC=12m\) và \(SO\) vuông góc với \(\left( {ABCD} \right)\). Làm tròn kết quả đến hàng đơn vị của Newton.