 Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
 Luyện tập chung trang 106 trang 106, 107, 108 Vở thực h..
Luyện tập chung trang 106 trang 106, 107, 108 Vở thực h..
Giải bài 1 trang 106 vở thực hành Toán 9 tập 2
Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.
Đề bài
Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.
Phương pháp giải - Xem chi tiết
+ Gọi M là trung điểm của BC.
+ Chứng minh \(ME = MB = MC = MF\). Suy ra đường tròn \(\left( {M,MB} \right)\) ngoại tiếp tứ giác \(BCEF\).
+ Chứng minh tương tự ta có \(CAFD\)và \(ABDE\) cũng là các tứ giác nội tiếp.
Lời giải chi tiết
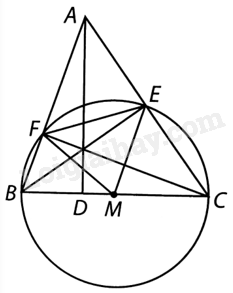
Lấy \(M\) là trung điểm của BC.
Do \(BCE,BCF\) là các tam giác vuông có chung cạnh huyền \(BC\) nên \(ME = MB = MC = MF\).
Do đó đường tròn \(\left( {M,MB} \right)\) ngoại tiếp tứ giác \(BCEF\).
Tương tự, \(CAFD\) và \(ABDE\) cũng là các tứ giác nội tiếp.
- Giải bài 2 trang 106 vở thực hành Toán 9 tập 2
- Giải bài 3 trang 107 vở thực hành Toán 9 tập 2
- Giải bài 4 trang 108 vở thực hành Toán 9 tập 2
- Giải bài 5 trang 108 vở thực hành Toán 9 tập 2
- Giải bài 6 trang 109 vở thực hành Toán 9 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay











