Đề thi học kì 2 Toán 9 - Đề số 5
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Cho hàm số \(y = \left( { - 2m + 1} \right){x^2}\). Tìm giá trị của \(m\) để đồ thị đi qua điểm \(A\left( { - 2;4} \right)\).
-
A.
m = 0.
-
B.
m = 1.
-
C.
m = 2.
-
D.
m = -2.
Phương trình \({x^2} - 2\sqrt {11} x + 3 = 0\) có \(\Delta '\) bằng
-
A.
8.
-
B.
7.
-
C.
9.
-
D.
10.
Cho phương trình \({x^2} + 7x - 15 = 0\) . Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình. Khi đó giá trị của biểu thức \(x_1^2 + x_2^2 - {x_1}{x_2}\)
-
A.
79.
-
B.
94.
-
C.
– 94.
-
D.
-79.
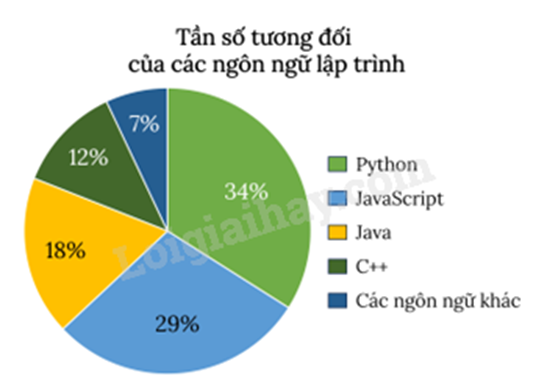
Biểu đồ hình quạt tròn dưới đây biểu diễn tần số tương đối của các ngôn ngữ lập trình được sử dụng khi viết 200 phần mềm của một công ty công nghệ. Biết rằng, mỗi phần mềm được viết bằng đúng một ngôn ngữ lập trình.
Ngôn ngữ lập trình nào được sử dụng phổ biến nhất khi viết 200 phần mềm đó:
-
A.
Python.
-
B.
JavaScript.
-
C.
C++.
-
D.
Java.
Cho tập hợp \(A = \left\{ {1;\,0;\,5;\,6} \right\}\). Bạn Mai dùng \(2\) chữ số khác nhau từ \(A\) để tạo thành số có \(2\) chữ số. Xác suất của biến cố “Số tạo thành chia hết cho \(5\)” là
-
A.
\(\frac{1}{2}\).
-
B.
\(\frac{5}{9}\).
-
C.
\(\frac{4}{9}\).
-
D.
\(\frac{1}{3}\).
Cho tam giác vuông cân ABC tại A có độ dài cạnh góc vuông 2 cm và nội tiếp đường tròn (O). Bán kính của đường tròn (O) là
-
A.
2 cm.
-
B.
4 cm.
-
C.
\(2\sqrt 2 \) cm.
-
D.
\(\sqrt 2 \) cm.
Cho hình vuông nội tiếp đường tròn (O; 5cm). Tính diện tích của hình vuông đó.
-
A.
\(10c{m^2}\).
-
B.
\(30c{m^2}\).
-
C.
\(40c{m^2}\).
-
D.
\(50c{m^2}\).
-
A.
Hình 1, 2, 3.
-
B.
Hình 1, 2, 3, 4.
-
C.
Hình 2, 3, 4.
-
D.
Hình 1, 3, 4.
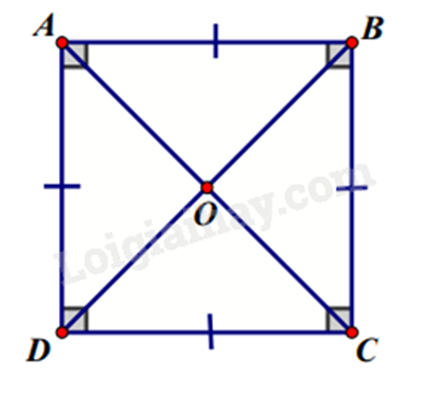
Cho hình vuông ABCD có tâm O . Phép quay thuận chiều kim đồng hồ \(180^\circ \) tâm O biến điểm A thành điểm nào?
-
A.
Điểm A.
-
B.
Điểm B.
-
C.
Điểm C.
-
D.
Điểm D.
Một hình trụ có chu vi đường tròn đáy bằng \(4\pi a\), chiều cao a. Thể tích của hình trụ này bằng
-
A.
\(4\pi {a^3}\).
-
B.
\(2\pi {a^3}\).
-
C.
\(16\pi {a^3}\).
-
D.
\(\frac{4}{3}\pi {a^3}\).
Cho hình nón có bán kính đáy \(\pi = \sqrt 3 cm\), độ dài đường sinh \(l = 4cm\). Tính diện tích xung quanh của hình nón đó?
-
A.
\(\sqrt {39} \pi \)\(\left( {c{m^2}} \right)\).
-
B.
\(4\sqrt 3 \pi \) \(\left( {c{m^2}} \right)\).
-
C.
\(12\pi \) \(\left( {c{m^2}} \right)\).
-
D.
\(8\sqrt 3 \pi \) \(\left( {c{m^2}} \right)\).
Cho hình cầu có thể tích là \(V = 972\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\). Tính đường kính của hình cầu.
-
A.
18cm.
-
B.
12cm.
-
C.
9cm.
-
D.
16cm.
Người ta hòa tan \(8kg\) chất lỏng loại 1 với \(6kg\) chất lỏng loại 2 thì được một hỗn hợp có khối lượng riêng là \(700kg/{m^3}\). Biết rằng khối lượng riêng của chất lỏng loại 1 lớn hơn khối lượng riêng của chất lỏng loại 2 là \(200kg/{m^3}\).
(Biết công thức tính khối lượng riêng: \(D = \frac{m}{V}\).
Trong đó: D là khối lượng riêng (\(kg/{m^3}\)), m là khối lượng của vật (kg) và V là thể tích (\({m^3}\))).
a) Gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\) thì điều kiện của x là \(x > 200\).
b) Thể tích của hỗn hợp 2 loại chất lỏng khi hòa tan là \(\frac{1}{{50}}\) \({m^3}\).
c) Gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\) thì phương trình với ẩn x là \(\frac{8}{x} + \frac{6}{{x + 200}} = \frac{1}{{50}}\).
d) Khối lượng riêng của chất lỏng loại 2 là \(800kg/{m^3}\).
Một hình nón có bán kính đáy bằng \(2\,cm\), chiều cao hình nón là \(h\,\,\left( {cm} \right)\).
a) Độ dài đường sinh của hình nón là \(\sqrt {{h^2} + 4} \,\,\,\left( {cm} \right)\).
b) Thể tích của hình nón là \(4\pi h\,\,\,\left( {c{m^3}} \right)\).
c) Diện tích toàn phần của hình nón là \({S_{tp}} = \pi .2\,.\sqrt {{h^2} + 4} + \pi {.2^2}\,\,\,\left( {c{m^2}} \right)\).
d) Chiều cao của hình nón trên bằng đường kính một hình cầu, diện tích toàn phần hình nón bằng diện tích mặt cầu. Chiều cao của hình nón là \(2\,\sqrt 3 \,cm\).
Cho hàm số \(y = \left( {3m - 1} \right){x^2}\) (m là tham số, \(m \ne 0,5\)). Biết rằng đồ thị hàm số đi qua điểm có hoành độ bằng 1 và tung độ bằng 2. Giá trị của m bằng bao nhiêu?
Đáp án:
Kết quả kiểm tra môn Toán giữa học kì 1 của học sinh lớp 9A được cho trong bảng tần số sau:

Tỉ lệ học sinh đạt điểm giỏi so với các học sinh còn lại là \(\frac{1}{a}\), giá trị của a là? (biết điểm giỏi là từ 8 điểm trở lên)
Đáp án:
Một hộp đựng ba viên bi màu xanh (ký hiệu X1, X2, X3) và hai viên bi màu vàng (ký hiệu V1, V2). Các viên bi đồng chất, giống nhau về hình dáng, có cùng kích thước và khối lượng. Bạn Thắng lấy ngẫu nhiên đồng thời hai viên bi từ trong hộp, các kết quả có thể xảy ra là đồng khả năng. Tính xác suất của biến cố A: “Bạn Thắng lấy được hai viên bi cùng màu".
Đáp án:
Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính 5cm. Độ dài cạnh AB bằng bao nhiêu cm?
Đáp án:
Lời giải và đáp án
Cho hàm số \(y = \left( { - 2m + 1} \right){x^2}\). Tìm giá trị của \(m\) để đồ thị đi qua điểm \(A\left( { - 2;4} \right)\).
-
A.
m = 0.
-
B.
m = 1.
-
C.
m = 2.
-
D.
m = -2.
Đáp án : A
Đồ thị hàm số đi qua điểm \(A\left( { - 2;4} \right)\) nên ta thay toạ độ điểm A vào hàm số để tìm m.
Để đồ thị đi qua điểm \(A\left( { - 2;4} \right)\) thì điểm A thuộc đồ thị hàm số \(y = \left( { - 2m + 1} \right){x^2}\).
Thay \(x = - 2;y = 4\) vào hàm số \(y = \left( { - 2m + 1} \right){x^2}\), ta được:
\(\begin{array}{l}4 = \left( { - 2m + 1} \right).{\left( { - 2} \right)^2}\\4 = 4\left( { - 2m + 1} \right)\\ - 2m + 1 = 1\\ - 2m = 0\\m = 0\end{array}\)
Vậy m = 0 thì đồ thị đi qua điểm \(A\left( { - 2;4} \right)\).
Đáp án A
Phương trình \({x^2} - 2\sqrt {11} x + 3 = 0\) có \(\Delta '\) bằng
-
A.
8.
-
B.
7.
-
C.
9.
-
D.
10.
Đáp án : A
Phương trình \(a{x^2} + bx + c = 0\) \((a \ne 0)\) với \(b' = \frac{b}{2}\) có hệ thức \(\Delta ' = b{'^2} - ac\).
Phương trình \({x^2} - 2\sqrt {11} x + 3 = 0\) có \(a = 1;b' = \frac{{ - 2\sqrt {11} }}{2} = - \sqrt {11} ;c = 3\) nên hệ thức \(\Delta ' = {\left( { - \sqrt {11} } \right)^2} - 1.3 = 11 - 3 = 8\).
Đáp án A
Cho phương trình \({x^2} + 7x - 15 = 0\) . Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình. Khi đó giá trị của biểu thức \(x_1^2 + x_2^2 - {x_1}{x_2}\)
-
A.
79.
-
B.
94.
-
C.
– 94.
-
D.
-79.
Đáp án : B
Xét sự tồn tại nghiệm của hai phương trình theo \(a.c\).
Sử dụng định lí Viète để biểu diễn \({x_1} + {x_2};{x_1}.{x_2}\) theo hệ số a, b, c.
Biến đổi biểu thức \(x_1^2 + x_2^2 - {x_1}{x_2}\) để xuất hiện \({x_1} + {x_2};{x_1}.{x_2}\) rồi tính giá trị của biểu thức.
Phương trình \({x^2} + 7x - 15 = 0\) có \(a.c = 1.\left( { - 15} \right) = - 15 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Áp dụng định lí Viète, ta có: \({x_1} + {x_2} = \frac{{ - 7}}{1} = - 7;{x_1}.{x_2} = \frac{{ - 15}}{1} = - 15\).
Ta có:
\(\begin{array}{l}x_1^2 + x_2^2 - {x_1}{x_2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - {x_1}{x_2}\\ = {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2}\\ = {\left( { - 7} \right)^2} - 3.\left( { - 15} \right)\\ = 49 + 45 = 94\end{array}\)
Vậy \(x_1^2 + x_2^2 - {x_1}{x_2} = 94\)
Đáp án B
Biểu đồ hình quạt tròn dưới đây biểu diễn tần số tương đối của các ngôn ngữ lập trình được sử dụng khi viết 200 phần mềm của một công ty công nghệ. Biết rằng, mỗi phần mềm được viết bằng đúng một ngôn ngữ lập trình.

Ngôn ngữ lập trình nào được sử dụng phổ biến nhất khi viết 200 phần mềm đó:
-
A.
Python.
-
B.
JavaScript.
-
C.
C++.
-
D.
Java.
Đáp án : A
So sánh tần số tương đối của các loại ngôn ngữ lập trình.
Ta có: 34% > 29% > 18% > 12% > 7% nên ngôn ngữ lập trình được sử dụng phổ biến nhất khi viết 200 phần mềm đó là Python (34%).
Đáp án A
Cho tập hợp \(A = \left\{ {1;\,0;\,5;\,6} \right\}\). Bạn Mai dùng \(2\) chữ số khác nhau từ \(A\) để tạo thành số có \(2\) chữ số. Xác suất của biến cố “Số tạo thành chia hết cho \(5\)” là
-
A.
\(\frac{1}{2}\).
-
B.
\(\frac{5}{9}\).
-
C.
\(\frac{4}{9}\).
-
D.
\(\frac{1}{3}\).
Đáp án : B
Xác định số phần tử của không gian mẫu.
Xác định các kết quả thuận lợi cho biến cố.
Khi đó xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố và số phần tử của không gian mẫu.
Không gian mẫu của phép thử là:
\(\Omega = \){10; 15; 16; 51; 50; 56; 61; 60; 65}
Không gian mẫu có 9 phần tử.
Kết quả thuận lợi cho biến cố “Số tạo thành chia hết cho \(5\)” là: 10; 15; 50; 60; 65.
Có 5 kết quả thuận lợi cho biến cố.
Vậy xác suất của biến cố “Số tạo thành chia hết cho \(5\)” là: \(\frac{5}{9}\).
Đáp án B
Cho tam giác vuông cân ABC tại A có độ dài cạnh góc vuông 2 cm và nội tiếp đường tròn (O). Bán kính của đường tròn (O) là
-
A.
2 cm.
-
B.
4 cm.
-
C.
\(2\sqrt 2 \) cm.
-
D.
\(\sqrt 2 \) cm.
Đáp án : D
Tính cạnh huyền của tam giác bằng định lí Pythagore.
Bán kính đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền.
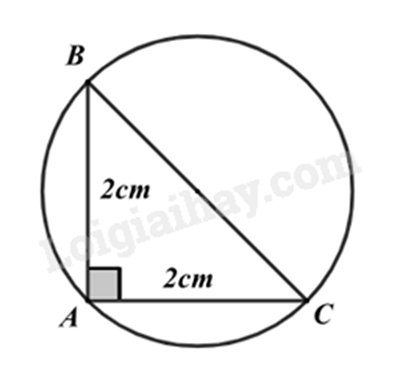
Áp dụng định lí Pythagore vào tam giác ABC vuông cân tại A, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {2^2} + {2^2} = 8\) suy ra \(BC = \sqrt 8 = 2\sqrt 2 \left( {cm} \right)\)
Do đó độ dài bán kính đường tròn ngoại tiếp tam giác ABC là: \(\frac{{2\sqrt 2 }}{2} = \sqrt 2 \left( {cm} \right)\).
Đáp án D
Cho hình vuông nội tiếp đường tròn (O; 5cm). Tính diện tích của hình vuông đó.
-
A.
\(10c{m^2}\).
-
B.
\(30c{m^2}\).
-
C.
\(40c{m^2}\).
-
D.
\(50c{m^2}\).
Đáp án : D
- Đường tròn ngoại tiếp của hình vuông có tâm là giao điểm của hai đường chéo và bán kính bằng một nửa độ dài đường chéo.
Ta tính được đường kính đường tròn = đường chéo của hình vuông.
- Sử dụng định lí Pythagore suy ra diện tích hình vuông: S = cạnh.cạnh.
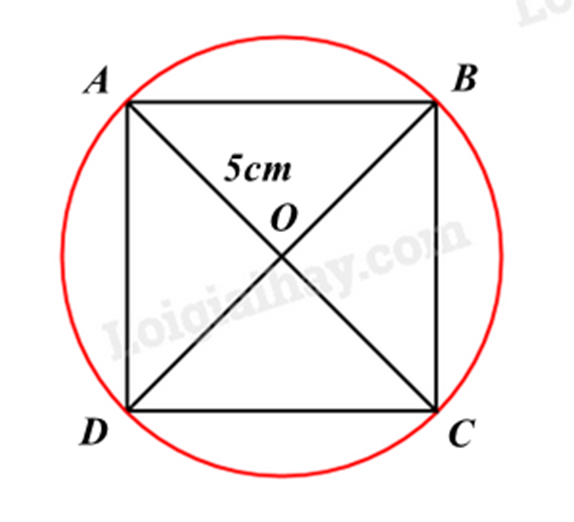
Vì bán kính đường tròn ngoại tiếp hình vuông là 5cm nên độ dài AC là: \(5.2 = 10\left( {cm} \right)\).
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B, ta có:
\(\begin{array}{l}A{B^2} + B{C^2} = A{C^2}\\2A{B^2} = {10^2}\\2A{B^2} = 100\\A{B^2} = 50\end{array}\)
Mà \({S_{hv}} = A{B^2}\) nên diện tích hình vuông ABCD là \(50c{m^2}\).
Đáp án D
-
A.
Hình 1, 2, 3.
-
B.
Hình 1, 2, 3, 4.
-
C.
Hình 2, 3, 4.
-
D.
Hình 1, 3, 4.
Đáp án : A
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.
Hình 1, 2, 3 là các hình có cấu trúc dạng hình phẳng đều là hình lục giác đều.
Hình 4 không có cấu trúc dạng hình phẳng đều.
Đáp án A
Cho hình vuông ABCD có tâm O . Phép quay thuận chiều kim đồng hồ \(180^\circ \) tâm O biến điểm A thành điểm nào?

-
A.
Điểm A.
-
B.
Điểm B.
-
C.
Điểm C.
-
D.
Điểm D.
Đáp án : C
Phép quay thuận chiều \(\alpha ^\circ \) tâm O biến điểm A thành điểm B.
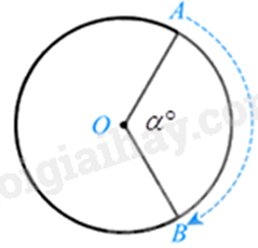
Phép quay thuận chiều kim đồng hồ \(180^\circ \) tâm O biến điểm A thành điểm đối xứng với nó qua O (quay một góc \(180^\circ \)) nên là điểm C.
Đáp án C
Một hình trụ có chu vi đường tròn đáy bằng \(4\pi a\), chiều cao a. Thể tích của hình trụ này bằng
-
A.
\(4\pi {a^3}\).
-
B.
\(2\pi {a^3}\).
-
C.
\(16\pi {a^3}\).
-
D.
\(\frac{4}{3}\pi {a^3}\).
Đáp án : A
Dựa vào chu vi đường tròn đáy để tính r.
Sử dụng công thức tính thể tích hình trụ: \(V = \pi {r^2}h\).
Vì chu vi đường tròn đáy của hình trụ bằng \(4\pi a\) nên \(2\pi r = 4\pi a\), suy ra \(r = 2a\).
Lại có \(h = a\) nên thể tích của hình trụ là:
\(V = \pi {r^2}h = \pi {\left( {2a} \right)^2}.a = 4\pi {a^3}\).
Đáp án A
Cho hình nón có bán kính đáy \(\pi = \sqrt 3 cm\), độ dài đường sinh \(l = 4cm\). Tính diện tích xung quanh của hình nón đó?
-
A.
\(\sqrt {39} \pi \)\(\left( {c{m^2}} \right)\).
-
B.
\(4\sqrt 3 \pi \) \(\left( {c{m^2}} \right)\).
-
C.
\(12\pi \) \(\left( {c{m^2}} \right)\).
-
D.
\(8\sqrt 3 \pi \) \(\left( {c{m^2}} \right)\).
Đáp án : B
Sử dụng công thức tính diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\).
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rl = \pi .\sqrt 3 .4 = 4\sqrt 3 \pi \left( {c{m^2}} \right)\)
Đáp án B
Cho hình cầu có thể tích là \(V = 972\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\). Tính đường kính của hình cầu.
-
A.
18cm.
-
B.
12cm.
-
C.
9cm.
-
D.
16cm.
Đáp án : A
Dựa vào công thức tính thể tích của hình cầu: \(V = \frac{4}{3}\pi {r^3}\) để tính bán kính r của hình cầu.
Từ đó suy ra đường kính của hình cầu: \(d = 2r\).
Vì hình cầu có thể tích là \(972\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\) nên ta có: \(972\pi = \frac{4}{3}\pi {r^3}\).
Do đó \({r^3} = \frac{{972\pi }}{{\frac{4}{3}\pi }} = 729\) suy ra \(r = \sqrt[3]{{729}} = 9\) (cm)
Đường kính của hình cầu là: 9.2 = 18 (cm)
Đáp án A
Người ta hòa tan \(8kg\) chất lỏng loại 1 với \(6kg\) chất lỏng loại 2 thì được một hỗn hợp có khối lượng riêng là \(700kg/{m^3}\). Biết rằng khối lượng riêng của chất lỏng loại 1 lớn hơn khối lượng riêng của chất lỏng loại 2 là \(200kg/{m^3}\).
(Biết công thức tính khối lượng riêng: \(D = \frac{m}{V}\).
Trong đó: D là khối lượng riêng (\(kg/{m^3}\)), m là khối lượng của vật (kg) và V là thể tích (\({m^3}\))).
a) Gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\) thì điều kiện của x là \(x > 200\).
b) Thể tích của hỗn hợp 2 loại chất lỏng khi hòa tan là \(\frac{1}{{50}}\) \({m^3}\).
c) Gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\) thì phương trình với ẩn x là \(\frac{8}{x} + \frac{6}{{x + 200}} = \frac{1}{{50}}\).
d) Khối lượng riêng của chất lỏng loại 2 là \(800kg/{m^3}\).
a) Gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\) thì điều kiện của x là \(x > 200\).
b) Thể tích của hỗn hợp 2 loại chất lỏng khi hòa tan là \(\frac{1}{{50}}\) \({m^3}\).
c) Gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\) thì phương trình với ẩn x là \(\frac{8}{x} + \frac{6}{{x + 200}} = \frac{1}{{50}}\).
d) Khối lượng riêng của chất lỏng loại 2 là \(800kg/{m^3}\).
a) Xác định điều kiện của \(x\) theo đề bài.
b) Tính thể tích của hỗn hợp = số kg : khối lượng riêng.
c) Gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\left( {x > 200} \right)\).
Biểu diễn khối lượng riêng của chất lỏng loại 2 theo \(x\).
Biểu diễn thể tích của chất lỏng loại 1 và thể tích của chất lỏng loại 2 theo \(x\).
Vì thể tích của hỗn hợp trước và sau khi trộn không đổi nên ta lập được phương trình.
c) Giải phương trình trên, kiểm tra lại nghiệm.
a) Đúng
Vì khối lượng riêng của chất lỏng loại 1 lớn hơn khối lượng riêng của chất lỏng loại 2.
Mà khối lượng riêng của chất lỏng loại 2 là \(200kg/{m^3}\)nên nếu gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\) thì \(x > 200\).
b) Đúng
Vì người ta hòa tan \(8kg\) chất lỏng loại 1 với \(6kg\) chất lỏng loại 2 thì được một hỗn hợp có khối lượng riêng là \(700kg/{m^3}\) nên thể tích của hỗn hợp là: \(\frac{{8 + 6}}{{700}} = \frac{{14}}{{700}} = \frac{1}{{50}}\left( {{m^3}} \right)\).
c) Sai
Gọi khối lượng riêng của chất lỏng loại 1 là \(x\left( {kg/{m^3}} \right)\left( {x > 200} \right)\).
khối lượng riêng của chất lỏng loại 2 là \(x-200\left( {kg/{m^3}} \right)\)
Do đó thể tích của chất lỏng loại 1 là \(\frac{8}{x}\;\left( {{m^3}} \right)\) và thể tích của chất lỏng loại 2 là \(\frac{6}{{x - 200}}\;\left( {{m^3}} \right)\) và thể tích của hỗn hợp là: \(\frac{{8 + 6}}{{700}} = \frac{{14}}{{700}} = \frac{1}{{50}}\left( {{m^3}} \right)\)
Vì thể tích của hỗn hợp trước và sau khi trộn không đổi nên ta có phương trình:
\(\frac{8}{x} + \frac{6}{{x - 200}} = \frac{1}{{50}}\)
d) Sai
Biến đổi phương trình về phương trình bậc hai một ẩn, ta được:
\(8.50\left( {x - 200} \right) + 6.50x = x\left( {x - 200} \right)\)
suy ra \({x^2} - 900x + 80000 = 0\)
Giải phương trình trên, ta được \({x_1} = 800\) (TMĐK) và \({x_2} = 100\)(loại)
Vậy khối lượng riêng của chất lỏng loại 1 là \(800kg/{m^3}\); khối lượng riêng của chất lỏng loại 2 là \(800-200 = 600\left( {kg/{m^3}} \right).\)
Đáp án: ĐĐSS
Một hình nón có bán kính đáy bằng \(2\,cm\), chiều cao hình nón là \(h\,\,\left( {cm} \right)\).
a) Độ dài đường sinh của hình nón là \(\sqrt {{h^2} + 4} \,\,\,\left( {cm} \right)\).
b) Thể tích của hình nón là \(4\pi h\,\,\,\left( {c{m^3}} \right)\).
c) Diện tích toàn phần của hình nón là \({S_{tp}} = \pi .2\,.\sqrt {{h^2} + 4} + \pi {.2^2}\,\,\,\left( {c{m^2}} \right)\).
d) Chiều cao của hình nón trên bằng đường kính một hình cầu, diện tích toàn phần hình nón bằng diện tích mặt cầu. Chiều cao của hình nón là \(2\,\sqrt 3 \,cm\).
a) Độ dài đường sinh của hình nón là \(\sqrt {{h^2} + 4} \,\,\,\left( {cm} \right)\).
b) Thể tích của hình nón là \(4\pi h\,\,\,\left( {c{m^3}} \right)\).
c) Diện tích toàn phần của hình nón là \({S_{tp}} = \pi .2\,.\sqrt {{h^2} + 4} + \pi {.2^2}\,\,\,\left( {c{m^2}} \right)\).
d) Chiều cao của hình nón trên bằng đường kính một hình cầu, diện tích toàn phần hình nón bằng diện tích mặt cầu. Chiều cao của hình nón là \(2\,\sqrt 3 \,cm\).
a) Sử dụng công thức liên hệ giữa đường sinh với bán kính đáy và chiều cao: \(l = \sqrt {{h^2} + {r^2}} \,\,\,\left( {cm} \right)\)
b) Sử dụng công thức tính thể tích hình nón: \(V = \frac{1}{3}\pi {R^2}h\).
c) Sử dụng công thức tính diện tích toàn phần của hình nón.
d) Tính diện tích mặt cầu. Lập phương trình và giải phương trình tìm h.
a) Đúng
Đường sinh của hình nón là:
\(l = \sqrt {{h^2} + {2^2}} = \sqrt {{h^2} + 4} \,\,\,\left( {cm} \right)\).
b) Sai
Thể tích của hình nón là:
\(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.2^2}h = \frac{4}{3}\pi h\,\,\,\left( {c{m^3}} \right)\)
c) Đúng
Diện tích toàn phần của hình nón là:
\({S_{tp}} = \pi .Rl + \pi .{R^2}\, = \)\(\pi .2\,.\sqrt {{h^2} + 4} + \pi {.2^2}\,\,\,\left( {c{m^2}} \right)\)
d) Đúng
Diện tích mặt cầu là: \(4\pi {\left( {\frac{h}{2}} \right)^2} = \pi {h^2}\)
Theo đề bài ta có:
\(\pi .2\,.\sqrt {{h^2} + 4} + \pi {.2^2}\,\, = \pi {h^2}\)
\(2\,.\sqrt {{h^2} + 4} + 4\, = {h^2}\)
\(2\,.\sqrt {{h^2} + 4} \, = {h^2} - 4\,\,\,\left( {h > 2} \right)\)
\(4\,.\left( {{h^2} + 4} \right)\, = {h^4} - 8\,h{\,^2} + 16\,\left( {h > 2} \right)\)
\(\begin{array}{l}{h^4} - 12{h^2} = 0\\{h^2}\left( {{h^2} - 12} \right) = 0\end{array}\)
\({h^2} = 0\) hoặc \({h^2} = 12\)
suy ra \(h = 0\,\,\,\left( L \right)\); \(h = - 2\sqrt 3 \,\,\,\left( L \right)\); \(h = 2\sqrt 3 \) (TM).
Vậy chiều cao của hình nón là \(2\,\sqrt 3 \,cm\).
Đáp án: ĐSĐĐ
Cho hàm số \(y = \left( {3m - 1} \right){x^2}\) (m là tham số, \(m \ne 0,5\)). Biết rằng đồ thị hàm số đi qua điểm có hoành độ bằng 1 và tung độ bằng 2. Giá trị của m bằng bao nhiêu?
Đáp án:
Đáp án:
Thay hoành độ bằng 1 và tung độ bằng 2 vào hàm số để tìm m.
Thay \(x = 1;y = 2\) vào \(y = \left( {3m - 1} \right){x^2}\), ta được:
\(\begin{array}{l}2 = 3m - 1\\3m = 3\\m = 1\left( {TM} \right)\end{array}\)
Đáp án: 1
Kết quả kiểm tra môn Toán giữa học kì 1 của học sinh lớp 9A được cho trong bảng tần số sau:

Tỉ lệ học sinh đạt điểm giỏi so với các học sinh còn lại là \(\frac{1}{a}\), giá trị của a là? (biết điểm giỏi là từ 8 điểm trở lên)
Đáp án:
Đáp án:
Xác định tỉ lệ học sinh đạt điểm giỏi so với các học sinh còn lại.
Từ đó tính được giá trị của a.
Tổng số học sinh đạt điểm giỏi là:
5 + 6 + 1 = 12 (học sinh)
Tổng số học sinh còn lại là:
0 + 0 + 1 + 2 + 6 + 7 + 8 = 24 (học sinh)
Vậy tỉ lệ học sinh đạt điểm giỏi so với các học sinh còn lại là:
\(\frac{{12}}{{24}} = \frac{1}{2}\). Do đó giá trị của a là 2.
Đáp án: 2
Một hộp đựng ba viên bi màu xanh (ký hiệu X1, X2, X3) và hai viên bi màu vàng (ký hiệu V1, V2). Các viên bi đồng chất, giống nhau về hình dáng, có cùng kích thước và khối lượng. Bạn Thắng lấy ngẫu nhiên đồng thời hai viên bi từ trong hộp, các kết quả có thể xảy ra là đồng khả năng. Tính xác suất của biến cố A: “Bạn Thắng lấy được hai viên bi cùng màu".
Đáp án:
Đáp án:
Xác định số phần tử của không gian mẫu, số kết quả thuận lợi cho biến cố.
Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi cho biến cố với số phần tử của không gian mẫu.
Không gian mẫu của phép thử là:
\(\Omega = \) {(X1, X2), (X1, X3), (X1, V1), (X1, V2), (X2, X3), (X2, V1), (X2, V2), (X3, V1), (X3, V2), (V1, V2)}.
Số phần tử của không gian mẫu là 10.
Các kết quả thuận lợi của biến cố A: “Bạn Thắng lấy được hai viên bi cùng màu" là:
(X1, X2), (X1, X3), (X2, X3), (V1, V2).
Có 4 kết quả thuận lợi cho biến cố B.
Do đó xác suất của biến cố B là:\(P(A) = \frac{4}{{10}} = \frac{2}{5} = 0,4\).
Đáp án: 0,4
Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính 5cm. Độ dài cạnh AB bằng bao nhiêu cm?
Đáp án:
Đáp án:
Tính số đo mỗi góc ở tâm ứng với một cạnh: \(\frac{{360^\circ }}{n}\) (với n là số cạnh của đa giác) suy ra tam giác AOB là tam giác đều.
Từ đó tính được độ dài AB.
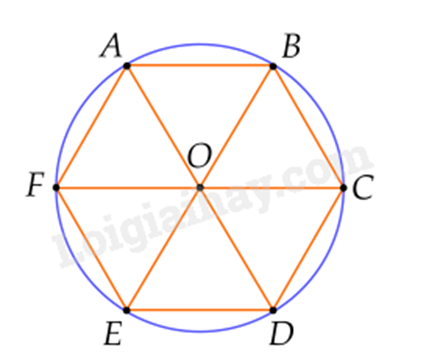
Ta có mỗi góc ở tâm ứng với mỗi cạnh của lục giác đều là:
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = \frac{{360^\circ }}{6} = 60^\circ \).
Mà AO = OB nên tam giác AOB là tam giác cân có một góc bằng \(60^\circ \) nên là tam giác đều.
Suy ra \(AB = 5cm\)
Đáp án: 5
a) Biểu diễn điểm có hoành độ và tung độ là hai số đối nhau.
Thay vào hàm số \(y = \frac{{ - 1}}{4}{x^2}\) để tìm các điểm thoả mãn.
b) Dùng \(ac < 0\) để xác định số nghiệm của phương trình.
Tính tổng và tích của hai nghiệm \({x_1},{x_2}\) theo định lí Viète: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - b}}{a}\\P = {x_1}{x_2} = \frac{c}{a}\end{array} \right.\).
Biến đổi biểu thức M để xuất hiện tổng và tích của hai nghiệm.
a) Gọi toạ độ điểm có hoành độ và tung độ là hai số đối nhau là \(\left( {{x_0}; - {x_0}} \right)\).
Vì \({y_0} = - {x_0}\) nên \( - {x_0} = \frac{{ - 1}}{4}x_0^2\)
\(\begin{array}{l}\frac{1}{4}x_0^2 - {x_0} = 0\\{x_0}\left( {\frac{1}{4}{x_0} - 1} \right) = 0\end{array}\)
\({x_0} = 0\) hoặc \(\frac{1}{4}{x_0} - 1 = 0\)
\({x_0} = 0\) hoặc \(\frac{1}{4}{x_0} = 1\)
\({x_0} = 0\) hoặc \({x_0} = 4\)
suy ra \({y_0} = 0\) hoặc \({y_0} = - 4\)
Do đó ta được \(\left( {0;0} \right)\) (loại) và \(\left( {4; - 4} \right)\).
Vậy điểm \(\left( {4; - 4} \right)\) thuộc \(\left( P \right):y = - \frac{1}{4}{x^2}\).
b) \(3{x^2} + 2x - 3 = 0\) có hai nghiệm phân biệt \({x_1};{x_2}\). Không giải phương trình, hãy tính giá trị biểu thức \(M = \left( {{x_1} - 2{x_2}} \right)\left( {{x_2} - {x_1}} \right) + x_2^2\).
Xét phương trình \(3{x^2} + 2x - 3 = 0\) ta có: \(ac = 3.\left( { - 3} \right) = - 9 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\).
Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = - \frac{2}{3}\\P = {x_1}.{x_2} = \frac{{ - 3}}{3} = - 1\end{array} \right.\)
Ta có: \(M = \left( {{x_1} - 2{x_2}} \right)\left( {{x_2} - {x_1}} \right) + x_2^2\)
\(\begin{array}{l} = {x_1}{x_2} - x_1^2 - 2x_2^2 + 2{x_1}{x_2} + x_2^2\\ = - x_1^2 + 3{x_1}{x_2} - x_2^2\\ = - \left( {x_1^2 + 2{x_1}{x_2} + x_2^2} \right) + 5{x_1}{x_2}\\ = - {\left( {{x_1} + {x_2}} \right)^2} + 5{x_1}{x_2}\\ = - {\left( { - \frac{2}{3}} \right)^2} + 5.\left( { - 1} \right)\\ = \frac{{ - 49}}{9}\end{array}\)
Vậy \(M = \frac{{ - 49}}{9}\).
a) Chứng minh \(\Delta IOD\) và \(\Delta IED\) nội tiếp đường tròn đường kính ID, do đó bốn điểm O, I, E, D thuộc đường tròn đường kính AB.
b) Chứng minh \(AH.\,AE = 2{R^2}\)
Chứng minh \(\Delta AHO\backsim \Delta ABE\) (g.g) suy ra \(\frac{{AH}}{{AO}} = \frac{{AB}}{{AE}}\), do đó \(AH \cdot AE = AO \cdot AB\).
Thay bằng R để tính \(AH.AE\).
Chứng minh \(OA = 3 \cdot OH\)
Tính OI, AI theo R.
Áp dụng tính chất đường phân giác của tam giác ABE để tính \(\frac{{AE}}{{BE}}\)
Vì \(\Delta AHO\backsim \Delta ABE\) nên \(\frac{{OA}}{{OH}} = \frac{{AE}}{{BE}}\) suy ra \(\frac{{OA}}{{OH}}\), suy ra điều phải chứng minh.
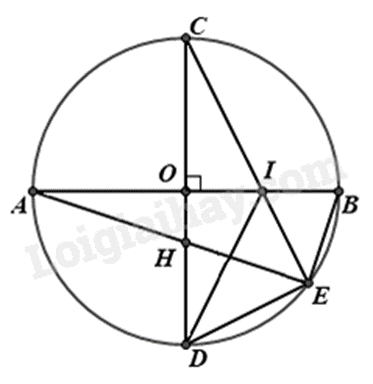
a) Xét \(\Delta IOD\) vuông tại O (\(CD \bot AB\) tại O) nên \(\Delta IOD\) nội tiếp đường tròn đường kính ID, do đó I, O, D thuộc đường tròn đường kính ID.
Xét \(\Delta IED\) vuông tại E (\(\widehat {CED} = 90^\circ \), góc nội tiếp chắn nửa đường tròn) nên \(\Delta IED\) nội tiếp đường tròn đường kính ID, do đó I, E, D thuộc đường tròn đường kính ID.
Do đó bốn điểm O, I, E, D thuộc đường tròn đường kính AB.
b) Chứng minh \(AH.\,AE = 2{R^2}\)
Ta có \(\widehat {AEB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét \(\Delta AHO\) và \(\Delta ABE\) có:
\(\widehat A\) chung
\(\widehat {AOH} = \widehat {AEB}\left( { = 90^\circ } \right)\)
nên \(\Delta AHO\backsim \Delta ABE\) (g.g) suy ra \(\frac{{AH}}{{AO}} = \frac{{AB}}{{AE}}\), do đó \(AH \cdot AE = AO \cdot AB = R \cdot 2R = 2{R^2}\)
Chứng minh \(OA = 3 \cdot OH\)
Vì I là trung điểm của OB nên $OI=\frac{1}{2}OB=\frac{1}{2}R$, suy ra $AI=R+\frac{1}{2}R=\frac{3}{2}R$
Vì $\widehat{AOC}=\widehat{COB}=90{}^\circ $ nên $\overset\frown{AC}=\overset\frown{CB}$, suy ra $\widehat{AEC}=\widehat{CEB}$ (góc nội tiếp chắn hai cung bằng nhau)
Do đó $EI$ là tia phân giác của góc $AEB$.
Vì $EI$ là tia phân giác của góc $AEB$ nên suy ra: $\frac{AE}{BE}=\frac{AI}{IB}=\frac{\frac{3}{2}R}{\frac{1}{2}R}=3$.
Vì $\Delta AHO\backsim \Delta ABE$ nên $\frac{OA}{OH}=\frac{AE}{BE}$ suy ra $\frac{OA}{OH}=3$, do đó $OA=3.OH$.
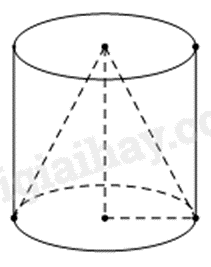
Sử dụng Viète để tính tổng và tích hai nghiệm của phương trình \({x^2} - 5x + 4 = 0\), suy ra bán kính và chiều cao của hình trụ.
Sử dụng công thức tính thể tích hình trụ và thể tích hình nón.
Thể tích gỗ tiện bỏ đi = thể tích hình trụ - thể tích hình nón.
Xét phương trình \({x^2} - 5x + 4 = 0\) ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.4 = 25 - 16 = 9 > 0\) nên phương trình có hai nghiệm \({x_1},{x_2}\).
Áp dụng định lí Viète, ta được: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{{ - 5}}{1} = 5\\{x_1}.{x_2} = \frac{4}{1} = 4\end{array} \right.\)
Do đó bán kính của hình trụ là 5 cm.
Chiều cao của hình trụ là: 3.4 = 12 (cm).
Thể tích khúc gỗ có dạng hình trụ là:
\({V_1} = \pi {r^2}h\approx 3,{14.5^2}.12 = 942\left( {c{m^3}} \right)\)
Thể tích khúc gỗ có dạng hình nón là
\({V_2} = \frac{1}{3}\pi {r^2}h\approx \frac{1}{3}.3,{14.5^2}.12 = 314\left( {c{m^3}} \right)\)
Thể tích gỗ tiện bỏ đi là
\(V = {V_1}-{V_2} \approx 942 - 314 = 628\left( {c{m^3}} \right)\)
Vậy thể tích gỗ tiện bỏ đi bằng khoảng \(628c{m^3}\).
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Các bài khác cùng chuyên mục
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5











Danh sách bình luận